题目内容
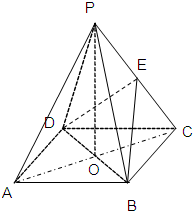 如图在四棱锥P-ABCD中,底面ABCD是正方形,O是正方形的中心,
如图在四棱锥P-ABCD中,底面ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,E是PC的中点.求证:
(1)PA∥平面BDE;
(2)AC⊥PB.
考点:直线与平面垂直的性质,直线与平面平行的判定
专题:空间位置关系与距离
分析:(1)通过证明PA∥EO,利用直线与平面平行的判定定理证明PA∥平面BDE;
(2)通过证明AC⊥平面PBD,利用直线与平面垂直的性质定理证明AC⊥PB.
(2)通过证明AC⊥平面PBD,利用直线与平面垂直的性质定理证明AC⊥PB.
解答:
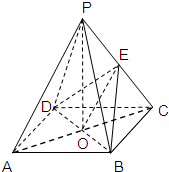 证明:(1)连接AC、OE,AC∩BD=O,在△PAC中,
证明:(1)连接AC、OE,AC∩BD=O,在△PAC中,
∵E为PC中点,O为AC中点.
∴PA∥EO,又∵EO?平面BDE,PA?平面BDE,∴PA∥平面BDE
(2)∵PO⊥底面ABCD,AC?平面ABCD∴PO⊥AC.
∵底面ABCD是正方形,∴BD⊥AC
又BD∩PO=O∴AC⊥平面PBD.
又PB?平面PBD,∴AC⊥PB
 证明:(1)连接AC、OE,AC∩BD=O,在△PAC中,
证明:(1)连接AC、OE,AC∩BD=O,在△PAC中,∵E为PC中点,O为AC中点.
∴PA∥EO,又∵EO?平面BDE,PA?平面BDE,∴PA∥平面BDE
(2)∵PO⊥底面ABCD,AC?平面ABCD∴PO⊥AC.
∵底面ABCD是正方形,∴BD⊥AC
又BD∩PO=O∴AC⊥平面PBD.
又PB?平面PBD,∴AC⊥PB
点评:本题考查直线与平面平行的判定定理以及直线与平面垂直的性质定理的应用,考查空间想象能力逻辑推理能力.

练习册系列答案
相关题目
五名学生和五名老师站成一排照相,五名老师不能相邻的排法有( )
A、2A
| ||||
B、A
| ||||
C、2A
| ||||
D、A
|
复数z=log2(m2-3m-3)+ilog2(3-m)(m∈R),如果a是纯虚数,则m的值为( )
| A、-1或4 | B、-1 | C、4 | D、3 |
若方程
=x(a∈R)在[-1,1]有解,则a的取值范围是( )
| 2x+x-a |
| A、[1,2] | ||
B、[-
| ||
| C、[1,3] | ||
D、[-
|