题目内容
若方程
=x(a∈R)在[-1,1]有解,则a的取值范围是( )
| 2x+x-a |
| A、[1,2] | ||
B、[-
| ||
| C、[1,3] | ||
D、[-
|
考点:根的存在性及根的个数判断
专题:函数的性质及应用
分析:由已知得2x=x2-x+a(a∈R)在[-1,1]有解,x<0时,方程
=x(a∈R)无解,从而方程
=x(a∈R)在[0,1]有解,由此能求出实数a的取值范围.
| 2x+x-a |
| 2x+x-a |
解答:
解:∵方程
=x(a∈R)在[-1,1]有解,
∴2x=x2-x+a(a∈R)在[-1,1]有解,
∵x<0时,方程
=x(a∈R)无解,
∴方程
=x(a∈R)在[0,1]有解,
∵x∈[0,1]时,2x∈[1,2],
设t=x2-x+a=(x-
)2+a-
,
∴x=0,tmin=a=1,
x=1时,tmax=(1-
)2+a-
=a=2,
∴实数a的取值范围是[1,2].
故选:A.
| 2x+x-a |
∴2x=x2-x+a(a∈R)在[-1,1]有解,
∵x<0时,方程
| 2x+x-a |
∴方程
| 2x+x-a |
∵x∈[0,1]时,2x∈[1,2],
设t=x2-x+a=(x-
| 1 |
| 2 |
| 1 |
| 4 |
∴x=0,tmin=a=1,
x=1时,tmax=(1-
| 1 |
| 2 |
| 1 |
| 4 |
∴实数a的取值范围是[1,2].
故选:A.
点评:本题考查实数的取值范围的求法,是中档题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
相关题目
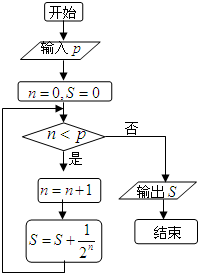
执行如图的程序框图,若输入的P是10,则输出的结果S的值为( )

A、1-
| ||
B、1-
| ||
C、1-
| ||
D、10-
|
过点(-l,3)且与直线x-2y+3=0垂直的直线方程是( )
| A、x-2y+7=0 |
| B、2x-y+5=0 |
| C、2x+y-5=0 |
| D、2x+y-1=0 |
设直线l1、l2的方向向量分别为
=(0,-3,3),
=(-1,1,0),则直线l1、l2的夹角是( )
| a |
| b |
| A、30° | B、45° |
| C、60° | D、120° |
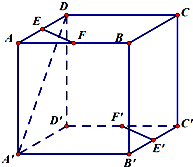 如图,在正方体AC′中,E,F,E′,F′分别是AD,AB,B′C′,D′C′的中点.
如图,在正方体AC′中,E,F,E′,F′分别是AD,AB,B′C′,D′C′的中点.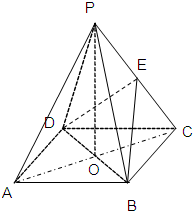 如图在四棱锥P-ABCD中,底面ABCD是正方形,O是正方形的中心,
如图在四棱锥P-ABCD中,底面ABCD是正方形,O是正方形的中心,