题目内容
已知双曲线两条渐近线的夹角为60°,求该双曲线的离心率是多少.
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:先由双曲线的两条渐近线的夹角为60°,得
=
或
,利用e2=1+(
)2,即可得到结论.
| b |
| a |
| 3 |
| ||
| 3 |
| b |
| a |
解答:
解:设双曲线方程为
-
=1(a>0,b>0),
由题意得
=
或
,
∴e2=1+(
)2=4或e2=
,
∴e=2或e=
.
| x2 |
| a2 |
| y2 |
| b2 |
由题意得
| b |
| a |
| 3 |
| ||
| 3 |
∴e2=1+(
| b |
| a |
| 4 |
| 3 |
∴e=2或e=
2
| ||
| 3 |
点评:本题主要考查了双曲线的性质.当涉及两直线的夹角问题时要注意考虑两个方面.

练习册系列答案
相关题目
过点(-l,3)且与直线x-2y+3=0垂直的直线方程是( )
| A、x-2y+7=0 |
| B、2x-y+5=0 |
| C、2x+y-5=0 |
| D、2x+y-1=0 |
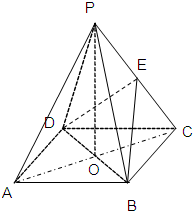 如图在四棱锥P-ABCD中,底面ABCD是正方形,O是正方形的中心,
如图在四棱锥P-ABCD中,底面ABCD是正方形,O是正方形的中心,