题目内容
4．从4台甲型和5台乙型电视机中任意取出2台，其中甲型与乙型电视机各1台，则不同的取法种数为20．分析 根据题意，分2步进行分析：①、先在4台甲型电视机取出1台，②、再在5台乙型电视机中取出1台，分别求出每一步的情况数目，由分步计数原理计算可得答案．
解答 解：根据题意，分2步进行分析：
①、先在4台甲型电视机取出1台，有4种取法；
②、再在5台乙型电视机中取出1台，有5种取法；
则有4×5=20种不同的取法；
故答案为：20．
点评 本题考查分步计数原理的应用，涉及组合数公式，注意分步分析满足题意的要求．
练习册系列答案
相关题目
18．$tan（-\frac{π}{4}）$=（ ）
| A． | 1 | B． | -1 | C． | $\frac{{\sqrt{2}}}{2}$ | D． | $-\frac{{\sqrt{2}}}{2}$ |
16．在区间[-1，1]上任取两数a、b，则关于x的二次方程x2+2ax+b=0有两个实数根的概率为（ ）
| A． | $\frac{π-2}{2}$ | B． | $\frac{4-π}{4}$ | C． | $\frac{π}{4}$ | D． | $\frac{2}{3}$ |
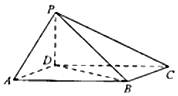如图，四棱锥P-ABCD中，底面ABCD为平行四边形，∠DAB=60°，AB=2AD，PD⊥底面ABCD．