题目内容
18．$tan（-\frac{π}{4}）$=（ ）| A． | 1 | B． | -1 | C． | $\frac{{\sqrt{2}}}{2}$ | D． | $-\frac{{\sqrt{2}}}{2}$ |
分析 由条件利用诱导公式化简所给的三角函数式，可得结果．
解答 解：$tan（-\frac{π}{4}）$=-tan$\frac{π}{4}$=-1，
故选：B．
点评 本题主要考查利用诱导公式进行化简求值，属于基础题．
练习册系列答案
相关题目
8．
执行如图程序框图，若输出y=2，则输入的x为（ ）
执行如图程序框图，若输出y=2，则输入的x为（ ）| A． | -1或$±\sqrt{2}$ | B． | ±1 | C． | 1或$\sqrt{2}$ | D． | $\sqrt{2}$ |
13．$\overrightarrow{a}$，$\overrightarrow{b}$都为向量，则下列式子正确的是（ ）
| A． | $\overrightarrow{a}$•|$\overrightarrow{a}$|=$\overrightarrow{a}$2 | B． | （$\overrightarrow{a}$•$\overrightarrow{b}$）2=$\overrightarrow{a}$2•$\overrightarrow{b}$2 | C． | （$\overrightarrow{a}$•$\overrightarrow{b}$）$\overrightarrow{c}$=$\overrightarrow{a}$（$\overrightarrow{b}$•$\overrightarrow{c}$） | D． | |$\overrightarrow{a}$•$\overrightarrow{b}$|≤|$\overrightarrow{a}$||$\overrightarrow{b}$| |
3．
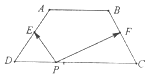如图，梯形ABCD中，AB∥CD，AB=2，CD=4，BC=AD=$\sqrt{5}$，E和F分别为AD与BC的中点，对于常数λ，在梯形ABCD的四条边上恰好有8个不同的点P，使得$\overrightarrow{PE}$•$\overrightarrow{PF}$=λ成立，则实数λ的取值范围是（ ）
如图，梯形ABCD中，AB∥CD，AB=2，CD=4，BC=AD=$\sqrt{5}$，E和F分别为AD与BC的中点，对于常数λ，在梯形ABCD的四条边上恰好有8个不同的点P，使得$\overrightarrow{PE}$•$\overrightarrow{PF}$=λ成立，则实数λ的取值范围是（ ）| A． | （-$\frac{5}{4}$，-$\frac{9}{20}$） | B． | （-$\frac{5}{4}$，$\frac{11}{4}$） | C． | （-$\frac{1}{4}$，$\frac{11}{4}$） | D． | （-$\frac{9}{20}$，-$\frac{1}{4}$） |
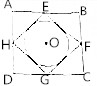已知四边形ABCD中，E，F，G，H分别是线段AB，BC，CD，DA的中点，圆O为四边形EFGH的内切圆，则在正方形ABCD内投一点，该点落在圆O内的概率为$\frac{π}{8}$．