题目内容
9.△ABC的内角A,B,C的对边分别为,且2acosC=2b-c.(1)求A的大小;
(2)若△ABC为锐角三角形,求sinB+sinC的取值范围;
(3)若$a=2\sqrt{3}$,且△ABC的面积为$2\sqrt{3}$,求cos2B+cos2C的值.
分析 (1)由余弦定理和夹角公式可得cosA=$\frac{1}{2}$,即可求出A的大小,
(2)求出角B的范围,再根据sinB+sinC=$\sqrt{3}$sin(B+$\frac{π}{6}$),利用正弦函数的性质即可求出范文,
(3)由余弦定理和三角形的面积公式求出b,c的值,再根据正弦定理即可求出B,C的值,问题得以解决
解答 解:(1)由余弦定理得:cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$,
∵2acosC=2b-c,
∴2a•$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$=2b-c,
即b2+c2-a2=ab,
∴cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$=$\frac{1}{2}$,
∵A∈(0,π),
∴A=$\frac{π}{3}$,
(2)∵△ABC为锐角三角形,
∴0<B,C<$\frac{π}{2}$,
∵C=$\frac{2π}{3}$-B,
∴$\frac{π}{6}$<B<$\frac{π}{2}$,
∵sinB+sinC=sinB+sin($\frac{2π}{3}$-B)=$\sqrt{3}$sin(B+$\frac{π}{6}$),
∵$\frac{π}{3}$<B+$\frac{π}{6}$<$\frac{2π}{3}$,
∴sin(B+$\frac{π}{6}$)∈($\frac{\sqrt{3}}{2}$,1],
∴sinB+sinC的取值范围为($\frac{3}{2}$,$\sqrt{3}$],
(3)在△ABC中,由余弦定理可得a2=b2+c2-2bccosA,
即12=b2+c2-bc ①,
∵△ABC的面积为$2\sqrt{3}$,
∴$\frac{1}{2}$bcsinA=2$\sqrt{3}$,
即bc=8,②,
由①②可得b=2,c=4,或b=4,c=2,
不放设b=2,c=4,
由正弦定理$\frac{a}{sinA}$=$\frac{b}{sinB}$=$\frac{c}{sinC}$=$\frac{2\sqrt{3}}{\frac{\sqrt{3}}{2}}$=4,
∴sinB=$\frac{1}{2}$,sinC=1,
∴B=$\frac{π}{6}$,C=$\frac{π}{2}$,
∴cos2B+cos2C=cos$\frac{π}{3}$+cosπ=$\frac{1}{2}$-1=-$\frac{1}{2}$
点评 本题考查了正弦定理余弦定理和三角形的面积公式以及三角函数的性质,考查了学生的运算能力和转化能力,属于中档题

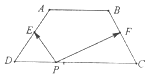 如图,梯形ABCD中,AB∥CD,AB=2,CD=4,BC=AD=$\sqrt{5}$,E和F分别为AD与BC的中点,对于常数λ,在梯形ABCD的四条边上恰好有8个不同的点P,使得$\overrightarrow{PE}$•$\overrightarrow{PF}$=λ成立,则实数λ的取值范围是( )
如图,梯形ABCD中,AB∥CD,AB=2,CD=4,BC=AD=$\sqrt{5}$,E和F分别为AD与BC的中点,对于常数λ,在梯形ABCD的四条边上恰好有8个不同的点P,使得$\overrightarrow{PE}$•$\overrightarrow{PF}$=λ成立,则实数λ的取值范围是( )| A. | (-$\frac{5}{4}$,-$\frac{9}{20}$) | B. | (-$\frac{5}{4}$,$\frac{11}{4}$) | C. | (-$\frac{1}{4}$,$\frac{11}{4}$) | D. | (-$\frac{9}{20}$,-$\frac{1}{4}$) |
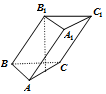 已知一三棱柱ABC-A1B1C1各棱长相等,B1在底面ABC上的射影是AC的中点,则异面直线AA1与BC所成角的余弦值为( )
已知一三棱柱ABC-A1B1C1各棱长相等,B1在底面ABC上的射影是AC的中点,则异面直线AA1与BC所成角的余弦值为( )| A. | $\frac{\sqrt{7}}{4}$ | B. | $\frac{3}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{4}{3}$ |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |