题目内容
已知函数f(x)是定义为在R上的奇函数,当x≥0时,f(x)=
(|x-a2|+|x-2a2|-3a2),若x∈R,都有f(x-1)≤f(x+1)成立,则实数a的取值范围是 .
| 1 |
| 2 |
考点:函数恒成立问题
专题:计算题,数形结合,分类讨论,函数的性质及应用
分析:由于当x≥0时,f(x)=
(|x-a2|+|x-2a2|-3a2).可得当0≤x≤a2时,f(x)=-x;当a2<x≤2a2时,f(x)=-a2;当x>3a2时,f(x)=x-3a2.画出其图象.由于函数f(x)是定义在R上的奇函数,即可画出x<0时的图象.由于x∈R,f(x-1)≤f(x+1),即有?x∈R,f(x-2)≤f(x),可得6a2≤2,解出即可.
| 1 |
| 2 |
解答:
解: ∵当x≥0时,f(x)=
∵当x≥0时,f(x)=
(|x-a2|+|x-2a2|-3a2).
∴当0≤x≤a2时,f(x)=
(a2-x+2a2-x-3a2)=-x;
当a2<x≤2a2时,f(x)=-a2;
当x>3a2时,f(x)=x-3a2.
画出其图象.
由于函数f(x)是定义在R上的奇函数,即可画出x<0时的图象,
与x>0时的图象关于原点对称.
∵?x∈R,f(x-1)≤f(x+1),
即有?x∈R,f(x-2)≤f(x),
∴6a2≤2,
解得-
≤a≤
.
∴实数a的取值范围为[-
,
].
故答案为:[-
,
].
 ∵当x≥0时,f(x)=
∵当x≥0时,f(x)=| 1 |
| 2 |
∴当0≤x≤a2时,f(x)=
| 1 |
| 2 |
当a2<x≤2a2时,f(x)=-a2;
当x>3a2时,f(x)=x-3a2.
画出其图象.
由于函数f(x)是定义在R上的奇函数,即可画出x<0时的图象,
与x>0时的图象关于原点对称.
∵?x∈R,f(x-1)≤f(x+1),
即有?x∈R,f(x-2)≤f(x),
∴6a2≤2,
解得-
| ||
| 3 |
| ||
| 3 |
∴实数a的取值范围为[-
| ||
| 3 |
| ||
| 3 |
故答案为:[-
| ||
| 3 |
| ||
| 3 |
点评:本题考查了函数奇偶性、周期性,考查了分类讨论的思想方法,考查了数形结合的思想方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
 如图所示的韦恩图中A,B是非空集合,定义集合A*B为阴影部分表示的集合,若x,y∈R,A={x|y=
如图所示的韦恩图中A,B是非空集合,定义集合A*B为阴影部分表示的集合,若x,y∈R,A={x|y=| 2x-x2 |
| A、{x|0<x<2} |
| B、{x|1<x<2} |
| C、{x|0≤x≤1或x≥2} |
| D、{x|0≤x≤1或x>2} |
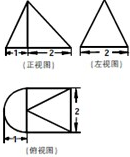
一个几何体的三视图如图,其俯视图是一个等边三角形,则这个几何体的体积为( )

A、
| ||||
B、
| ||||
C、
| ||||
D、(4+π)
|
“m=1”是“直线mx+(2m-1)y+1=0和直线3x+my-3=0垂直”的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |