题目内容
4.已知函数f(x)=x4-4x3+10x2-27,则方程f(x)=0在[2,10]上的根( )| A. | 有3个 | B. | 有2个 | C. | 有且只有1个 | D. | 不存在 |
分析 先求导f′(x)=4x3-12x2+20x=4x[(x-$\frac{3}{2}$)2+$\frac{11}{4}$],从而得到函数f(x)=x4-4x3+10x2-27在[2,10]上单调递增,再由函数零点的判定定理从而求得方程f(x)=0在[2,10]上的根的个数.
解答 解:∵f(x)=x4-4x3+10x2-27,
∴f′(x)=4x3-12x2+20x
=4x[(x-$\frac{3}{2}$)2+$\frac{11}{4}$],
∴f(x)=x4-4x3+10x2-27在[2,10]上单调递增,
又∵f(2)=16-32+40-27=-3,
f(10)=10000-4000+1000-27=6963,
故方程f(x)=0在[2,10]上的根的个数为1个.
故选:C
点评 本题考查了导数的综合应用,同时考查了函数零点的判定定理,属于中档题.

练习册系列答案
相关题目
5.要得到函数y=3cos2x的图象,只需将函数$y=3cos({2x+\frac{π}{3}})$的图象( )
| A. | 向左平移$\frac{π}{3}$个单位长度 | B. | 向右平移$\frac{π}{3}$个单位长度 | ||
| C. | 向左平移$\frac{π}{6}$个单位长度 | D. | 向右平移$\frac{π}{6}$个单位长度 |
16.设f(x)为定义在R上的奇函数,当x≥0时,f(x)=2x+2x+b,则b为( )
| A. | -1 | B. | 0 | C. | 1 | D. | 无法确定 |
13.全集U=R,集合A={x|-1≤x≤1且x≠0},B={x|x<-1或x>4},则A∩(∁UB)=( )
| A. | {x|-2≤x<4} | B. | {x|x≤3或x≥4} | C. | {x|-1≤x≤1且x≠0} | D. | {x|-1≤x≤3} |
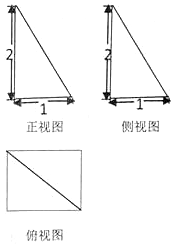 已知四棱锥P-ABCD,PA⊥底面ABCD,其三视图如下,若M是PD的中点.
已知四棱锥P-ABCD,PA⊥底面ABCD,其三视图如下,若M是PD的中点.