题目内容
14.已知正项数列{an}的前n项和为Sn,当n≥2时,(an-Sn-1)2=SnSn-1,且a1=1,设bn=log2$\frac{{a}_{n+1}}{6}$,则bn等于( )| A. | 2n-3 | B. | 2n-4 | C. | n-3 | D. | n-4 |
分析 先根据数列的递推公式得到(Sn-2Sn-1)2=SnSn-1,即可得到$\frac{{S}_{n}}{{S}_{n-1}}$+$\frac{4{S}_{n-1}}{{S}_{n}}$=5,解得Sn=4Sn-1,即可求出数列an的通项公式,再根据对数的运算性质即可求出答案.
解答 解:∵an=Sn-Sn-1,$({a}_{n}-{S}_{n-1})^{2}={S}_{n}{S}_{n-1}$,
∴(Sn-2Sn-1)2=SnSn-1,
∴Sn2+4Sn-12=5SnSn-1,
∴$\frac{{S}_{n}}{{S}_{n-1}}$+$\frac{4{S}_{n-1}}{{S}_{n}}$=5,
令$\frac{{S}_{n}}{{S}_{n-1}}$=t,
∴t+$\frac{4}{t}$=5,
解得t=1或t=4,
∴Sn=Sn-1,或Sn=4Sn-1,
∵正项数列{an}的前n项和为Sn,
∴Sn≠Sn-1,
∴Sn=4Sn-1,
∵S1=a1=1,
∴{Sn}是以1为首项,以4为公比的等比数列,
∴Sn=4n-1,
当n=1时,S1=a1=1,
当n≥2时,an+1=Sn+1-Sn=4n-4n-1=3×4n-1,
∴$\frac{{a}_{n+1}}{6}$=$\frac{3×{4}^{n-1}}{6}$=22n-3,
∴bn=log2$\frac{{a}_{n+1}}{6}$=2n-3,
故选:A.
点评 本题考查了数列的递推公式求出数列的通项公式以及等比数列的性质,考查了学生的运算能力,转化能力,属于中档题.

练习册系列答案
相关题目
4.已知函数f(x)=x4-4x3+10x2-27,则方程f(x)=0在[2,10]上的根( )
| A. | 有3个 | B. | 有2个 | C. | 有且只有1个 | D. | 不存在 |
2.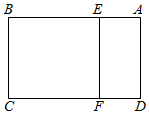 如图,在矩形ABCD中,AD=$\sqrt{5}$,AB=3,E、F分别为AB边、CD边上一点,且AE=DF=l,现将矩形ABCD沿EF折起,使得平面ADFE⊥平面BCFE,连接AB、CD,则所得三棱柱ABE-DCF的侧面积比原矩形ABCD的面积大约多(取$\sqrt{5}$≈2.236)( )
如图,在矩形ABCD中,AD=$\sqrt{5}$,AB=3,E、F分别为AB边、CD边上一点,且AE=DF=l,现将矩形ABCD沿EF折起,使得平面ADFE⊥平面BCFE,连接AB、CD,则所得三棱柱ABE-DCF的侧面积比原矩形ABCD的面积大约多(取$\sqrt{5}$≈2.236)( )
 如图,在矩形ABCD中,AD=$\sqrt{5}$,AB=3,E、F分别为AB边、CD边上一点,且AE=DF=l,现将矩形ABCD沿EF折起,使得平面ADFE⊥平面BCFE,连接AB、CD,则所得三棱柱ABE-DCF的侧面积比原矩形ABCD的面积大约多(取$\sqrt{5}$≈2.236)( )
如图,在矩形ABCD中,AD=$\sqrt{5}$,AB=3,E、F分别为AB边、CD边上一点,且AE=DF=l,现将矩形ABCD沿EF折起,使得平面ADFE⊥平面BCFE,连接AB、CD,则所得三棱柱ABE-DCF的侧面积比原矩形ABCD的面积大约多(取$\sqrt{5}$≈2.236)( )| A. | 68% | B. | 70% | C. | 72% | D. | 75% |
9. 某程序框图如图所示,若输入输出的n分别为3和1,则在图中空白的判断框中应填入的条件可以为( )
某程序框图如图所示,若输入输出的n分别为3和1,则在图中空白的判断框中应填入的条件可以为( )
 某程序框图如图所示,若输入输出的n分别为3和1,则在图中空白的判断框中应填入的条件可以为( )
某程序框图如图所示,若输入输出的n分别为3和1,则在图中空白的判断框中应填入的条件可以为( )| A. | i≥7? | B. | i>7? | C. | i≥6? | D. | i<6? |
19.当a>0,a≠1时,函数f(x)=loga(x-1)+1的图象恒过定点A,若点A在直线mx-y+n=0上,则4m+2n的最小值是( )
| A. | 4 | B. | $2\sqrt{2}$ | C. | $\sqrt{2}$ | D. | 2 |
6.设函数f(x)=$\left\{\begin{array}{l}{log_3}x,0<x≤9\\ f(x-4),x>9\end{array}$则$f(13)+2f(\frac{1}{3})$的值为( )
| A. | 1 | B. | 0 | C. | -2 | D. | 2 |
3.抛物线y2=12x上与焦点的距离等于9的点的坐标( )
| A. | $(6,±6\sqrt{2})$ | B. | $(6\sqrt{2},±6)$ | C. | $(12,±6\sqrt{2})$ | D. | $(6\sqrt{2},±12)$ |