题目内容
9.已知函数$f(x)={log_4}({{4^x}+1})+kx$是偶函数.(1)求k的值;
(2)若函数$h(x)={4^{f(x)+\frac{1}{2}x}}+m×{2^x}-1,x∈[{0,{{log}_2}3}]$,是否存在实数m使得h(x)最小值为0,若存在,求出m的值;若不存在,请说明理由.
分析 (1)根据函数是偶函数,即f(-x)=f(x),可得k的值.
(2)求解出h(x),转化为二次函数,利用对称轴讨论其最小值,可得结论.
解答 解:(1)由题意,函数$f(x)={log_4}({{4^x}+1})+kx$是偶函数.
∵f(-x)=f(x),
即${log_4}({{4^{-x}}+1})-kx={log_4}({{4^x}+1})+kx$对于任意x∈R恒成立,
∴$2kx={log_4}({{4^{-x}}+1})-{log_4}({{4^x}+1})={log_4}\frac{{{4^{-x}}+1}}{{{4^x}+1}}$,
∴2kx=-x,
∴$k=-\frac{1}{2}$.
(2)由题意,h(x)=4x+m×2x,x∈[0,log23],
令t=2x∈[1,3],φ(t)=t2+mt,t∈[1,3],开口向上,对称轴$t=-\frac{m}{2}$,
当$-\frac{m}{2}≤1$,即m≥-2时,φ(t)min=φ(1)=1+m=0,解得:m=-1,
当$1<-\frac{m}{2}<3$,即-6<m<-2时,$φ{(t)_{min}}=φ({-\frac{m}{2}})=-\frac{m^2}{4}=0,m=0$(舍去),
当$-\frac{m}{2}>3$,即m<-6时,φ(t)min=φ(3)=9+3m=0,∴m=-3(舍去)
∴存在m=-1使得h(x)最小值为0.
点评 本题考查了对数的基本运算和二次函数的最值的讨论求解参数问题.属于中档题.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
4.已知函数f(x)=x4-4x3+10x2-27,则方程f(x)=0在[2,10]上的根( )
| A. | 有3个 | B. | 有2个 | C. | 有且只有1个 | D. | 不存在 |
9. 某程序框图如图所示,若输入输出的n分别为3和1,则在图中空白的判断框中应填入的条件可以为( )
某程序框图如图所示,若输入输出的n分别为3和1,则在图中空白的判断框中应填入的条件可以为( )
 某程序框图如图所示,若输入输出的n分别为3和1,则在图中空白的判断框中应填入的条件可以为( )
某程序框图如图所示,若输入输出的n分别为3和1,则在图中空白的判断框中应填入的条件可以为( )| A. | i≥7? | B. | i>7? | C. | i≥6? | D. | i<6? |
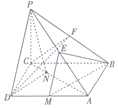 如图,在四棱锥P-ABCD中,PC⊥底面ABCD,底面ABCD是矩形,BC=PC,E,F分别是PA,PB的中点.
如图,在四棱锥P-ABCD中,PC⊥底面ABCD,底面ABCD是矩形,BC=PC,E,F分别是PA,PB的中点. 如图,已知平面ABC⊥平面BCDE,△DEF与△ABC分别是棱长为1与2的正三角形,AC∥DF,四边形BCDE为直角梯形,DE∥BC,BC⊥CD,CD=1,点G为△ABC的重心,N为AB中点,$\overrightarrow{AM}=λ\overrightarrow{AF}(λ∈R,λ>0)$.
如图,已知平面ABC⊥平面BCDE,△DEF与△ABC分别是棱长为1与2的正三角形,AC∥DF,四边形BCDE为直角梯形,DE∥BC,BC⊥CD,CD=1,点G为△ABC的重心,N为AB中点,$\overrightarrow{AM}=λ\overrightarrow{AF}(λ∈R,λ>0)$.