Question

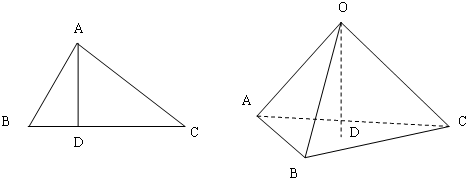
△ABC中，∠A=90°，过点A作BC边上的高AD，则

1

AD2

=

1

AB2

+

1

AC2

，请利用上述结论，类比推出，在空间四面体O-ABCD中，若OA，OB，OC两两垂直，O到平面ABC的距离为OD，则

 

．

Answer 1

考点：类比推理

专题：推理和证明

分析：本题根据条件特征，分析表达式的结构特点，进行类比，得到相关结论，还可以利用代数法加以证明，对于平面三角形，利用面积公式进行证明，对于空间四面体，可以利用体积公式进行证明，得到本题结论．

解答： 解：∵△ABC中，∠A=90°，过点A作BC边上的高AD，则

1

AD2

=

1

AB2

+

1

AC2

，
空间四面体O-ABCD中，若OA，OB，OC两两垂直，空间四面体O-ABCD中，
∴由△ABC中，过三角顶点A，BC边上的高AD，类比，对应的是空间四面体O-ABCD中，过直角顶点作空间四面体O-ABCD中，
由

1

AD2

=

1

AB2

+

1

AC2

，类比知，平方的倒数和的关系，得到

1

OD2

=

1

OA2

+

1

OB2

+

1

OC2

．
故答案为：

1

OD2

=

1

OA2

+

1

OB2

+

1

OC2

．

点评：本题考查了类比推理，本题难度不大，属于基础题．