题目内容
6.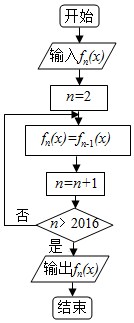 如图程序框图中,当n∈N*(n>1)时,函数fn(x)表示函数fn-1(x)的导函数,即fn(x)=f′n-1(x).若输入函数f1(x)=sinx+cosx,则输出的函数fn(x)为( )
如图程序框图中,当n∈N*(n>1)时,函数fn(x)表示函数fn-1(x)的导函数,即fn(x)=f′n-1(x).若输入函数f1(x)=sinx+cosx,则输出的函数fn(x)为( )| A. | $\sqrt{2}sin(x+\frac{π}{4})$ | B. | $-\sqrt{2}sin(x+\frac{π}{4})$ | C. | $\sqrt{2}sin(x-\frac{π}{4})$ | D. | $-\sqrt{2}sin(x-\frac{π}{4})$ |
分析 由已知中的程序框图可知:该程序的功能是利用循环结构计算并输出函数fn(x),模拟程序的运行过程,分析循环中各变量值的变化情况,可得答案.
解答 解:∵函数f1(x)=sinx+cosx,fn(x)=f′n-1(x).
∴第1次执行循环体后,f2(x)=-sinx+cosx,n=3,不满足退出循环的条件;
第2次执行循环体后,f3(x)=-sinx-cosx,n=4,不满足退出循环的条件;
第3次执行循环体后,f4(x)=sinx-cosx,n=5,不满足退出循环的条件;
第4次执行循环体后,f5(x)=sinx+cosx,n=6,不满足退出循环的条件;
第5次执行循环体后,f6(x)=-sinx+cosx,n=7,不满足退出循环的条件;
…
第2014次执行循环体后,f2015(x)=-sinx-cosx,n=2016,不满足退出循环的条件;
第2015次执行循环体后,f2016(x)=sinx-cosx,n=2017,不满足退出循环的条件;
故输出的函数为:f2016(x)=sinx-cosx=$\sqrt{2}sin(x-\frac{π}{4})$,
故选:C
点评 本题考查的知识点是程序框图,当循环的次数不多,或有规律时,常采用模拟循环的方法解答.

练习册系列答案
相关题目
1.极坐标方程分别是ρ=2cosθ和ρ=2sinθ的两个圆的圆心距是( )
| A. | 2 | B. | $\sqrt{2}$ | C. | 1 | D. | $\frac{{\sqrt{2}}}{2}$ |
11.庄子说:“一尺之锤,日取其半.万世不竭”.这句话描述的问题实质是一个等比数列,设等比数列{an}的首项a1=1,前n项和Sn,则Sn一定满足( )
| A. | Sn>$\frac{3}{2}$ | B. | Sn<$\frac{3}{2}$ | C. | Sn>2 | D. | Sn<2 |