题目内容
14．已知圆C的极坐标方程是ρ=4sinθ以极点为平面直角坐标系的原点，极轴为x轴的正半轴，建立平面直角坐标系．（1）求圆C的直角坐标方程和圆心和圆心C的极坐标；
（2）若斜率为2，且过点P（0，a）的直线l与圆C相交于A，B两点，且|PA|•|PB|=3，求实数a的值．
分析 （1）将极坐标方程两边同乘ρ，得到直角坐标方程；
（2）求出直线l的参数方程，代入圆的普通方程，根据参数得几何意义和根与系数的关系列出方程解出a．
解答 解：（1）∵ρ=4sinθ，∴ρ2=4ρsinθ，即x2+y2-4y=0．
∴圆C的直角坐标方程为x2+（y-2）2=4．圆心C（0，2）．
∴圆心C的极坐标为（2，$\frac{π}{2}$）．
（2）直线l的参数方程为$\left\{\begin{array}{l}{x=\frac{t}{\sqrt{5}}}\\{y=a+\frac{2t}{\sqrt{5}}}\end{array}\right.$（t为参数）．
将直线l的参数方程代入x2+（y-2）2=4得t2+$\frac{4a-8}{\sqrt{5}}t+{a}^{2}-4a=0$．
∴|PA|•|PB|=|t1t2|=|a2-4a|=3．
解得a=1或3或2$±\sqrt{7}$．
点评 本题考查了极坐标方程与直角坐标方程的转化，参数方程的几何意义，属于基础题．
练习册系列答案
备战中考寒假系列答案
相关题目
4．若区间（0，1）上任取一实数b，则方程x2+x+b=0有实根的概率为（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{3}{4}$ |
5．
把一副三角板ABC与ABD摆成如图所示的直二面角D-AB-C，（其中BD=2AD，BC=AC）则异面直线DC，AB所成角的正切值为（ ）
把一副三角板ABC与ABD摆成如图所示的直二面角D-AB-C，（其中BD=2AD，BC=AC）则异面直线DC，AB所成角的正切值为（ ）| A． | $\sqrt{3}$ | B． | $\sqrt{7}$ | C． | $\frac{{\sqrt{21}}}{7}$ | D． | $\frac{{\sqrt{21}}}{3}$ |
2．设数列{an}是公差大于0的等差数列，且a8+a9+…+a12=0，则前n项和Sn最小时n的值为（ ）
| A． | 9 | B． | 10 | C． | 9或10 | D． | 19 |
19．设Sn是等差数列{an}的前n项和，若a1+a3+a5=3，则S5=（ ）
| A． | 5 | B． | 7 | C． | 9 | D． | 11 |
6．
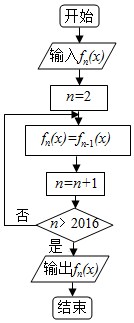如图程序框图中，当n∈N*（n＞1）时，函数fn（x）表示函数fn-1（x）的导函数，即fn（x）=f′n-1（x）．若输入函数f1（x）=sinx+cosx，则输出的函数fn（x）为（ ）
如图程序框图中，当n∈N*（n＞1）时，函数fn（x）表示函数fn-1（x）的导函数，即fn（x）=f′n-1（x）．若输入函数f1（x）=sinx+cosx，则输出的函数fn（x）为（ ）| A． | $\sqrt{2}sin（x+\frac{π}{4}）$ | B． | $-\sqrt{2}sin（x+\frac{π}{4}）$ | C． | $\sqrt{2}sin（x-\frac{π}{4}）$ | D． | $-\sqrt{2}sin（x-\frac{π}{4}）$ |