题目内容
1．极坐标方程分别是ρ=2cosθ和ρ=2sinθ的两个圆的圆心距是（ ）| A． | 2 | B． | $\sqrt{2}$ | C． | 1 | D． | $\frac{{\sqrt{2}}}{2}$ |
分析 求出两圆的普通方程和圆心坐标，代入两点间的距离公式计算．
解答 解：两圆的直角坐标方程分别为（x-1）2+y2=1，x2+（y-1）2=1．
∴两圆的圆心分别是（1，0），（0，1）．
∴两圆的圆心距为$\sqrt{2}$．
故选：B．
点评 本题考查了极坐标方程与直角坐标方程的转化，属于基础题．
练习册系列答案
手拉手全优练考卷系列答案
相关题目
11．函数y=-x2+1的单调递增区间为（ ）
| A． | （-∞，0] | B． | [0，+∞） | C． | （0，+∞） | D． | （-∞，+∞） |
6．
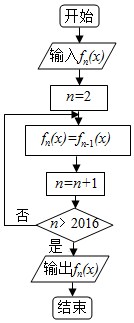如图程序框图中，当n∈N*（n＞1）时，函数fn（x）表示函数fn-1（x）的导函数，即fn（x）=f′n-1（x）．若输入函数f1（x）=sinx+cosx，则输出的函数fn（x）为（ ）
如图程序框图中，当n∈N*（n＞1）时，函数fn（x）表示函数fn-1（x）的导函数，即fn（x）=f′n-1（x）．若输入函数f1（x）=sinx+cosx，则输出的函数fn（x）为（ ）| A． | $\sqrt{2}sin（x+\frac{π}{4}）$ | B． | $-\sqrt{2}sin（x+\frac{π}{4}）$ | C． | $\sqrt{2}sin（x-\frac{π}{4}）$ | D． | $-\sqrt{2}sin（x-\frac{π}{4}）$ |
13．如图是一个程序框图，它的功能是（ ）
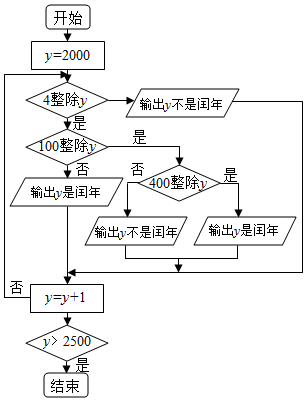
| A． | 输出年份y∈[2000，2500）且y∈N“哪年是闰年”“哪年不是闰年” | |
| B． | 输出年份y∈[2000，2500]且y∈N“哪年是闰年”“哪年不是闰年” | |
| C． | 输出年份y∈[2000，2500）且y∈N“多少年是闰年”“多少年不是闰年” | |
| D． | 输出年份y∈[2000，2500]且y∈N“多少年是闰年”“多少年不是闰年” |
10．若直线4x+3y+1=0的斜率为k，在y轴上的截距为b，则（ ）
| A． | k=-$\frac{4}{3}$，b=$\frac{1}{3}$ | B． | k=-$\frac{4}{3}$，b=-$\frac{1}{3}$ | C． | k=$\frac{4}{3}$，b=$\frac{1}{3}$ | D． | k=$\frac{4}{3}$，b=-$\frac{1}{3}$ |