题目内容
18．设x，y满足约束条件$\left\{\begin{array}{l}{1≤x≤2}\\{2≤x+2y≤4}\\{\;}\end{array}\right.$，则（x+1）2+（y+2）2的取值范围为[$\frac{41}{4}$，18]．分析 作平面区域，从而可得（1+1）2+（$\frac{1}{2}$+2）2≤（x+1）2+（y+2）2≤（2+1）2+（1+2）2，从而解得．
解答 解：作平面区域如下，
，
由图象可得，A（1，$\frac{1}{2}$），B（2，1），
故（1+1）2+（$\frac{1}{2}$+2）2≤（x+1）2+（y+2）2≤（2+1）2+（1+2）2，
故$\frac{41}{4}$≤（x+1）2+（y+2）2≤18，
故答案为：[$\frac{41}{4}$，18]．
点评 本题考查了线性规划的应用及数形结合的思想应用．
练习册系列答案
相关题目
8．中心在原点，一焦点为F1（0，c）的椭圆被直线y=3x-2截得的弦的中点横坐标是$\frac{1}{2}$，则此椭圆的离心率为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{{\sqrt{6}}}{3}$ | C． | $\frac{{\sqrt{5}}}{3}$ | D． | $\frac{2}{3}$ |
6．
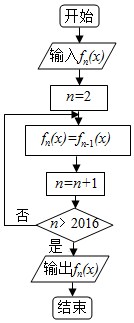如图程序框图中，当n∈N*（n＞1）时，函数fn（x）表示函数fn-1（x）的导函数，即fn（x）=f′n-1（x）．若输入函数f1（x）=sinx+cosx，则输出的函数fn（x）为（ ）
如图程序框图中，当n∈N*（n＞1）时，函数fn（x）表示函数fn-1（x）的导函数，即fn（x）=f′n-1（x）．若输入函数f1（x）=sinx+cosx，则输出的函数fn（x）为（ ）| A． | $\sqrt{2}sin（x+\frac{π}{4}）$ | B． | $-\sqrt{2}sin（x+\frac{π}{4}）$ | C． | $\sqrt{2}sin（x-\frac{π}{4}）$ | D． | $-\sqrt{2}sin（x-\frac{π}{4}）$ |
13．如图是一个程序框图，它的功能是（ ）
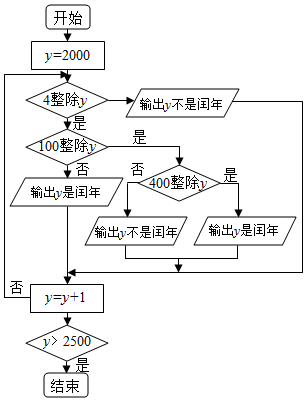
| A． | 输出年份y∈[2000，2500）且y∈N“哪年是闰年”“哪年不是闰年” | |
| B． | 输出年份y∈[2000，2500]且y∈N“哪年是闰年”“哪年不是闰年” | |
| C． | 输出年份y∈[2000，2500）且y∈N“多少年是闰年”“多少年不是闰年” | |
| D． | 输出年份y∈[2000，2500]且y∈N“多少年是闰年”“多少年不是闰年” |
10．若直线4x+3y+1=0的斜率为k，在y轴上的截距为b，则（ ）
| A． | k=-$\frac{4}{3}$，b=$\frac{1}{3}$ | B． | k=-$\frac{4}{3}$，b=-$\frac{1}{3}$ | C． | k=$\frac{4}{3}$，b=$\frac{1}{3}$ | D． | k=$\frac{4}{3}$，b=-$\frac{1}{3}$ |