题目内容
16.已知椭圆E:$\frac{x^2}{8}$+$\frac{y^2}{4}$=1,A、B分别是椭圆E的左、右顶点,动点M在射线1:x=4$\sqrt{2}$(y>0)上运动,MA交椭圆E于点P,MB交椭圆E于点Q.(1)若△MAB垂心的纵坐标为-4$\sqrt{7}$,求点的P坐标;
(2)试问:直线PQ是否过定点?若过定点,求出定点坐标;若不过定点,请说明理由.
分析 (1)设M(4$\sqrt{2}$,m),由A(-2$\sqrt{2}$,0),B(2$\sqrt{2}$,0),垂心H(4$\sqrt{2}$,-4$\sqrt{7}$),由BH⊥MA,运用直线斜率公式和斜率之积为-1,可得m,再由直线MA与椭圆求得交点P;
(2)设M(4$\sqrt{2}$,m),由A(-2$\sqrt{2}$,0),B(2$\sqrt{2}$,0),可得MA的方程为y=$\frac{m}{6\sqrt{2}}$(x+2$\sqrt{2}$),代入椭圆方程,运用韦达定理,解得P的坐标;同理求得Q的坐标,运用直线的斜率公式可得PQ的斜率,由点斜式方程可得PQ的方程,再由恒过定点思想,即可得到所求定点.
解答 解:(1)设M(4$\sqrt{2}$,m),由A(-2$\sqrt{2}$,0),B(2$\sqrt{2}$,0),
垂心H(4$\sqrt{2}$,-4$\sqrt{7}$),由BH⊥MA,可得
kBH•kMA=-1,即有$\frac{4\sqrt{7}}{-2\sqrt{2}}$•$\frac{m}{6\sqrt{2}}$=-1,
可得m=$\frac{6}{\sqrt{7}}$,
由MA的方程:y=$\frac{1}{\sqrt{14}}$(x+2$\sqrt{2}$),代入椭圆方程,可得
8x2+4$\sqrt{2}$x-48=0,
解得x=-2$\sqrt{2}$,或$\frac{3\sqrt{2}}{2}$,即有P($\frac{3\sqrt{2}}{2}$,$\frac{\sqrt{7}}{2}$);
(2)设M(4$\sqrt{2}$,m),由A(-2$\sqrt{2}$,0),B(2$\sqrt{2}$,0),
可得MA的方程为y=$\frac{m}{6\sqrt{2}}$(x+2$\sqrt{2}$),代入椭圆方程,可得
(36+m2)x2+4$\sqrt{2}$m2x+8m2-288=0,
由-2$\sqrt{2}$xP=$\frac{8{m}^{2}-288}{36+{m}^{2}}$,可得xP=$\frac{(72-2{m}^{2})\sqrt{2}}{36+{m}^{2}}$,
yP=$\frac{m}{6\sqrt{2}}$(xP+2$\sqrt{2}$)=$\frac{24m}{36+{m}^{2}}$;
又MB:y=$\frac{m}{2\sqrt{2}}$(x-2$\sqrt{2}$),代入椭圆方程,可得
(4+m2)x2-4$\sqrt{2}$m2x+8m2-32=0,
由2$\sqrt{2}$+xQ=$\frac{4\sqrt{2}{m}^{2}}{4+{m}^{2}}$,可得xQ=$\frac{(2{m}^{2}-8)\sqrt{2}}{4+{m}^{2}}$,
yQ=$\frac{m}{2\sqrt{2}}$(xQ-2$\sqrt{2}$)=-$\frac{8m}{4+{m}^{2}}$,
即有直线PQ的斜率为k=$\frac{{y}_{Q}-{y}_{P}}{{x}_{Q}-{x}_{P}}$=$\frac{8m}{\sqrt{2}(12-{m}^{2})}$,
则直线PQ:y-$\frac{24m}{36+{m}^{2}}$=$\frac{8m}{\sqrt{2}(12-{m}^{2})}$(x-$\frac{(72-2{m}^{2})\sqrt{2}}{36+{m}^{2}}$),
化简即有y=$\frac{8m}{12-{m}^{2}}$($\frac{\sqrt{2}}{2}$x-1),
由$\frac{\sqrt{2}}{2}$x-1=0,解得x=$\sqrt{2}$,y=0.
故直线PQ恒过定点($\sqrt{2}$,0).
点评 本题考查椭圆的方程和性质,主要考查直线方程和椭圆方程联立,运用韦达定理,同时考查直线方程的运用以及直线的斜率公式,考查运算能力,属于中档题.

 小学教材全测系列答案
小学教材全测系列答案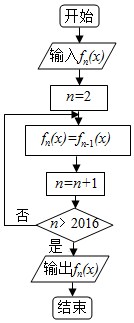 如图程序框图中,当n∈N*(n>1)时,函数fn(x)表示函数fn-1(x)的导函数,即fn(x)=f′n-1(x).若输入函数f1(x)=sinx+cosx,则输出的函数fn(x)为( )
如图程序框图中,当n∈N*(n>1)时,函数fn(x)表示函数fn-1(x)的导函数,即fn(x)=f′n-1(x).若输入函数f1(x)=sinx+cosx,则输出的函数fn(x)为( )| A. | $\sqrt{2}sin(x+\frac{π}{4})$ | B. | $-\sqrt{2}sin(x+\frac{π}{4})$ | C. | $\sqrt{2}sin(x-\frac{π}{4})$ | D. | $-\sqrt{2}sin(x-\frac{π}{4})$ |
| A. | 1 | B. | 2 | C. | $\sqrt{5}$ | D. | 3 |