题目内容
17.已知圆C的一条直径上的两个端点的坐标为(1,1),(1,5).(1)求圆C的标准方程;
(2)求直线3x-4y+4=0截圆C所得弦长l的值;
(3)从圆C外一点P(a,b)向圆C引切线PT,T为切点,使|PT|=|PO|(O为原点),求|PT|的最小值.
分析 (1)求出圆心坐标,和半径即可得到结论.
(2)根据直线和圆相交的弦长公式进行求解即可.
(3)根据条件建立方程关系进行求解即可.
解答 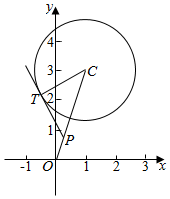 解:(1)圆心坐标为C($\frac{1+1}{2}$,$\frac{1+5}{2}$),即C(1,2),2r=|5-1|=4,即半径r=2,
解:(1)圆心坐标为C($\frac{1+1}{2}$,$\frac{1+5}{2}$),即C(1,2),2r=|5-1|=4,即半径r=2,
则圆C的标准方程为(x-1)2+(y-3)2=4.
(2)圆心C到直线3x-4y+4=0的距离d=$\frac{|3-4×3+4|}{\sqrt{{3}^{2}+{4}^{2}}}$=1,
则弦长L=2$\sqrt{{r}^{2}-{d}^{2}}=2\sqrt{{2}^{2}-{1}^{1}}=2\sqrt{3}$.
(3)∵C(1,3),半径r=2,
∴作切线PT,连接PC,CT,由平面几何知识得|PT|2=|PC|2-|CT|2=(a-1)2+(b-3)2-4,
∵|PT|=|PO|,
∴(a-1)2+(b-3)2-4=a2+b2,
得a+3b-3=0,
|PT|min=|PO|min=$\frac{|-3|}{\sqrt{{1}^{2}+{3}^{2}}}$=$\frac{3\sqrt{10}}{10}$.
点评 本题主要考查圆的标准方程以及直线和圆的位置关系的应用,考查学生的运算和推理能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.设集合M={0,1,2},N={x∈N|x-1≥0},则M∩N=( )
| A. | {1} | B. | {2} | C. | {0,1} | D. | {1,2} |
8.中心在原点,一焦点为F1(0,c)的椭圆被直线y=3x-2截得的弦的中点横坐标是$\frac{1}{2}$,则此椭圆的离心率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{6}}}{3}$ | C. | $\frac{{\sqrt{5}}}{3}$ | D. | $\frac{2}{3}$ |
5. 把一副三角板ABC与ABD摆成如图所示的直二面角D-AB-C,(其中BD=2AD,BC=AC)则异面直线DC,AB所成角的正切值为( )
把一副三角板ABC与ABD摆成如图所示的直二面角D-AB-C,(其中BD=2AD,BC=AC)则异面直线DC,AB所成角的正切值为( )
 把一副三角板ABC与ABD摆成如图所示的直二面角D-AB-C,(其中BD=2AD,BC=AC)则异面直线DC,AB所成角的正切值为( )
把一副三角板ABC与ABD摆成如图所示的直二面角D-AB-C,(其中BD=2AD,BC=AC)则异面直线DC,AB所成角的正切值为( )| A. | $\sqrt{3}$ | B. | $\sqrt{7}$ | C. | $\frac{{\sqrt{21}}}{7}$ | D. | $\frac{{\sqrt{21}}}{3}$ |
2.设数列{an}是公差大于0的等差数列,且a8+a9+…+a12=0,则前n项和Sn最小时n的值为( )
| A. | 9 | B. | 10 | C. | 9或10 | D. | 19 |
6.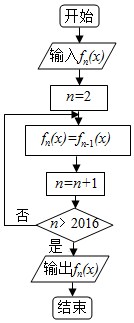 如图程序框图中,当n∈N*(n>1)时,函数fn(x)表示函数fn-1(x)的导函数,即fn(x)=f′n-1(x).若输入函数f1(x)=sinx+cosx,则输出的函数fn(x)为( )
如图程序框图中,当n∈N*(n>1)时,函数fn(x)表示函数fn-1(x)的导函数,即fn(x)=f′n-1(x).若输入函数f1(x)=sinx+cosx,则输出的函数fn(x)为( )
 如图程序框图中,当n∈N*(n>1)时,函数fn(x)表示函数fn-1(x)的导函数,即fn(x)=f′n-1(x).若输入函数f1(x)=sinx+cosx,则输出的函数fn(x)为( )
如图程序框图中,当n∈N*(n>1)时,函数fn(x)表示函数fn-1(x)的导函数,即fn(x)=f′n-1(x).若输入函数f1(x)=sinx+cosx,则输出的函数fn(x)为( )| A. | $\sqrt{2}sin(x+\frac{π}{4})$ | B. | $-\sqrt{2}sin(x+\frac{π}{4})$ | C. | $\sqrt{2}sin(x-\frac{π}{4})$ | D. | $-\sqrt{2}sin(x-\frac{π}{4})$ |