Question

利用计算机在区间（0，1）上产生两个随机数a和b，则函数y=x+

b

x

-2

a

有零点的概率为（　　）

• A、

  1

  2

• B、

  1

  3

• C、

  2

  3

• D、1

Answer 1

考点：几何概型

专题：概率与统计

分析：求出函数y=x+

b

x

-2

a

有零点的等价条件，利用几何概型的概率公式求出相应的区域面积即可得到结论．

解答： 解：函数y=x+

b

x

-2

a

=

x2-2 a x+b

x

，
要使函数y=x+

b

x

-2

a

有零点，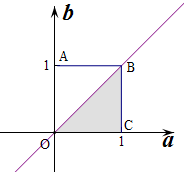
则等价为x²-2

a

x+b=0有解，
即△=4a-4b≥0，
∴a-b≥0，
∵

0＜a＜1 0＜b＜1

，
∴作出对应的平面区域如图：
则函数y=x+

b

x

-2

a

有零点对应的区域为△OAB，对应的面积S=

1

2

×1×1=

1

2

，
∴根据几何概型的概率公式可得y=x+

b

x

-2

a

有零点的概率为

1 2

1×1

=

1

2

，
故选：A．

点评：本题主要考查几何概型的概率计算，求出函数y=x+

b

x

-2

a

有零点的等价条件是解决本题的关键．