题目内容
实数a,b两数中最小值用min{a,b}表示,若函数f(x)=min{x2,(x-m)2}(m为常数)的图象关于直线x=1对称,则函数f(x)在[0,4]上的值域是 .
考点:函数的值域
专题:计算题,函数的性质及应用
分析:根据已知条件及函数的对称性,求出m,进而得出函数的解析式及已知x的范围求得y的范围.
解答:
解:当x=0时,min{x2,(x-m)2}=min{0,m2}=0
∴f(0)=0
∵f(x)=min{x2,(x-m)2}(m为常数)的图象关于直线x=1对称,
∴f(2)=f(0)=0
∴min{22,(2-m)2}=0
根据min{a,b}表的定义,只能有2-m=0
∴m=2
∴f(x)=min{x2,(x-2)2}
①当x∈[0,1]时,|x|<|x-2|,即x2<(x-2)2,
则f(x)=min{x2,(x-2)2}=x2,
∵函数f(x)=x2在区间[0,1]上单调增,
∴f(x)∈[0,1]
②当x∈[1,4]时,|x|<|x-2|,即x2>(x-2)2,
则f(x)=min{x2,(x-2)2}=(x-2)2,
函数f(x)=(x-2)2在区间[1,4]时,当x=2时有最小值0,当x=4时,f(x)有最大值4,
∴f(x)∈[0,4]
综合①②可知函数f(x)在[0,4]时,f(x)∈[0,4]
故答案为:[0,4]
∴f(0)=0
∵f(x)=min{x2,(x-m)2}(m为常数)的图象关于直线x=1对称,
∴f(2)=f(0)=0
∴min{22,(2-m)2}=0
根据min{a,b}表的定义,只能有2-m=0
∴m=2
∴f(x)=min{x2,(x-2)2}
①当x∈[0,1]时,|x|<|x-2|,即x2<(x-2)2,
则f(x)=min{x2,(x-2)2}=x2,
∵函数f(x)=x2在区间[0,1]上单调增,
∴f(x)∈[0,1]
②当x∈[1,4]时,|x|<|x-2|,即x2>(x-2)2,
则f(x)=min{x2,(x-2)2}=(x-2)2,
函数f(x)=(x-2)2在区间[1,4]时,当x=2时有最小值0,当x=4时,f(x)有最大值4,
∴f(x)∈[0,4]
综合①②可知函数f(x)在[0,4]时,f(x)∈[0,4]
故答案为:[0,4]
点评:本题主要考查了函数的值域问题及分段函数.分段函数的函数值和相关不等式是高考的常考点.用好分类讨论和数形结合的思想,可起到事半功倍的效果.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案
相关题目
执行如图所示的程序框图,如输入x=2,则输出的值为( )


| A、5 |
| B、log85 |
| C、9 |
| D、log89 |
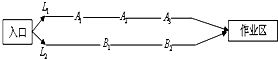 某煤矿发生透水事故时,作业区有若干人员被困.救援队从入口进入之后有L1,L2两条巷道通往作业区(如图),L1巷道有A1,A2,A3三个易堵塞点,各点被堵塞的概率都是
某煤矿发生透水事故时,作业区有若干人员被困.救援队从入口进入之后有L1,L2两条巷道通往作业区(如图),L1巷道有A1,A2,A3三个易堵塞点,各点被堵塞的概率都是