题目内容
已知函数y=f(x+t)的值域为[3,5],则函数y=2f(x)的值域为 .
考点:函数的值域
专题:常规题型,函数的性质及应用
分析:先根据已知条件推断出函数y=f(x)的值域,进而推断出y=2f(x),得出答案.
解答:
∵函数y=f(x)的图象由函数y=f(x+t)的图象平移得到,
∴函数y=f(x)的值域与函数y=f(x+t)的值域向同,为[3,5],
∵函数y=2f(x)的图象由函数y=f(x)的图象,横坐标不变,纵坐标扩大2倍获得的,
∴函数y=2f(x)图象中的最大值和最小值,分别为函数y=f(x)最大值和最小值的2倍,
∴函数y=2f(x)的值域为[6,10]
故答案为:[6,10]
∴函数y=f(x)的值域与函数y=f(x+t)的值域向同,为[3,5],
∵函数y=2f(x)的图象由函数y=f(x)的图象,横坐标不变,纵坐标扩大2倍获得的,
∴函数y=2f(x)图象中的最大值和最小值,分别为函数y=f(x)最大值和最小值的2倍,
∴函数y=2f(x)的值域为[6,10]
故答案为:[6,10]
点评:本题主要考查了学生对函数的值域以及函数图象的变换的理解和应用.

练习册系列答案
相关题目
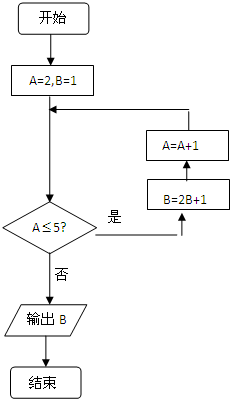
执行如图所示的程序框图,则输出的n的值是( )


| A、43 | B、44 | C、45 | D、46 |