题目内容
8.△ABC的内角A,B,C的对边a,b,c满足a2+ac=b2.(Ⅰ)求A的取值范围;
(Ⅱ)若a=2,A=$\frac{π}{6}$,求△ABC的面积.
分析 (1)由余弦定理得a2-b2=c2-2bccosA,由a2+ac=b2得a2-b2=-ac,故c2-2bccosA=-ac,即cosA=$\frac{a+c}{2b}$,因为a+c>b,所以cosA$>\frac{1}{2}$,得出A的范围;
(2)将A=$\frac{π}{6}$和a=2分别代入a2+ac=b2和b2+c2-a2=2bccosA,联立方程组解出b,c,使用S=$\frac{1}{2}$bcsinA求出面积.
解答 解:(1)由余弦定理得a2=b2+c2-2bccosA,∴a2-b2=c2-2bccosA,又∵a2+ac=b2,∴a2-b2=-ac.
∴c2-2bccosA=-ac,∴cosA=$\frac{a+c}{2b}$,∵a+c>b,∴cosA$>\frac{1}{2}$.∴0<A<$\frac{π}{3}$.
(2)∵a2+ac=b2,∴4+2c=b2,∵b2+c2-a2=2bccosA,∴b2+c2-4=$\sqrt{3}$bc,
联立方程组$\left\{\begin{array}{l}{4+2c={b}^{2}}\\{{b}^{2}+{c}^{2}-4=\sqrt{3}bc}\end{array}\right.$,解得b=2$\sqrt{3}$,c=4.
S△ABC=$\frac{1}{2}$bcsinA=$\frac{1}{2}×2\sqrt{3}×4×\frac{1}{2}$=2$\sqrt{3}$.
点评 本题考查了余弦定理在解三角形中的应用,属于中档题.

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
18.在复平面内,复数$\frac{2}{1-i}$-2对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
3.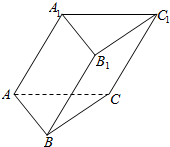 如图,在三棱柱ABC-A1B1C1中,各棱长均相等,且∠A1AB=∠A1AC=∠BAC=60°,则AB1与底面ABC所成角的正弦值为( )
如图,在三棱柱ABC-A1B1C1中,各棱长均相等,且∠A1AB=∠A1AC=∠BAC=60°,则AB1与底面ABC所成角的正弦值为( )
 如图,在三棱柱ABC-A1B1C1中,各棱长均相等,且∠A1AB=∠A1AC=∠BAC=60°,则AB1与底面ABC所成角的正弦值为( )
如图,在三棱柱ABC-A1B1C1中,各棱长均相等,且∠A1AB=∠A1AC=∠BAC=60°,则AB1与底面ABC所成角的正弦值为( )| A. | $\frac{1}{3}$ | B. | $\frac{\sqrt{2}}{3}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{1}{2}$ |
13.在正四棱锥P-ABCD中,PA=2,E为PC的中点,若异面直线PA与BE所成角为45°,则四棱锥P-ABCD的高为( )
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |