题目内容

18．在复平面内，复数$\frac{2}{1-i}$-2对应的点位于（　　）
A．第一象限B．第二象限C．第三象限D．第四象限

分析 利用复数的运算法则、几何意义即可得出．

解答 解：复数$\frac{2}{1-i}$-2=$\frac{2（1+i）}{（1-i）（1+i）}$-2=-1+i对应的点（-1，1）位于第二象限．
故选：B．

点评 本题考查了复数的运算法则、几何意义，考查了推理能力与计算能力，属于基础题．

练习册系列答案
相关题目
8．在${（x+\frac{2}{x^2}）^6}$的展开式中，常数项为60．（用数字作答）
9．已知一几何体的三视图如下，则该几何体的表面积为3+$\sqrt{5}$．
6．已知极坐标系的极点在平面直角坐标系的原点O处，极轴与x轴的正半轴重合，且长度单位相同，直线l的极坐标方程为：ρ=$\frac{5}{sin（θ-\frac{π}{3}）}$，点P（2cosα，2sinα+2），参数α∈R．
（Ⅰ）求点P轨迹的直角坐标方程；
（Ⅱ）求点P到直线l距离的最大值．
13．在复平面内，复数$\frac{2}{1-i}$-2i2对应的点位于（　　）
A．第一象限B．第二象限C．第三象限D．第四象限
3．为了解某校学生的视力情况，现采用随机抽样的方式从该校的A，B两班中各抽5名学生进行视力检测，检测的数据如下：
A班5名学生的视力检测结果：4.3，5.1，4.6，4.1，4.9．
B班5名学生的视力检测结果：5.1，4.9，4.0，4.0，4.5．
（1）分别计算两组数据的平均数，从计算结果看，哪个班的学生视力较好？并计算A班5名学生视力的方差；
（2）现从B班的上述5名学生中随机选取2名，求这2名学生中至少有1名学生的视力低于4.5的概率．
10．已知直线y=k（x-1）及抛物线y2=2x，则（　　）
A．直线与抛物线有且只有一个公共点B．直线与抛物线有两个公共点
C．直线与抛物线有一个或两个公共点D．直线与抛物线可能没有公共点
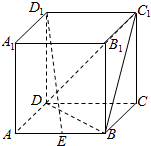7．如图，已知正方体ABCD-A1B1C1D1的棱长为2，点E为棱AB的中点．
求：（1）点C到面BC1D的距离；
（2）D1E与平面BC1D所成角的正弦值．
8．△ABC的内角A，B，C的对边a，b，c满足a2+ac=b2．
（Ⅰ）求A的取值范围；
（Ⅱ）若a=2，A=$\frac{π}{6}$，求△ABC的面积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网