题目内容
对于函数f(x)=a-
(a∈R).
(1)确定f(x)的单调区间;
(2)求实数a,使f(x)是奇函数,在此基础上,求f(x)的值域.
| 2 |
| ex+1 |
(1)确定f(x)的单调区间;
(2)求实数a,使f(x)是奇函数,在此基础上,求f(x)的值域.
考点:函数奇偶性的性质,函数的单调性及单调区间
专题:函数的性质及应用
分析:(1)先求函数的定义域,再对函数求导,由导数的符号确定函数的单调区间;
(2)由f(x)是奇函数,得f(0)=0,从而a-
=a-1=0,可得a=1,把a代入函数的表达式再求函数的值域.
(2)由f(x)是奇函数,得f(0)=0,从而a-
| 2 |
| e0+1 |
解答:
解:(1)∵对任意实数x,函数都有意义,∴函数的定义域为(-∞,+∞),
f′(x)=-
=
>0恒成立,∴f(x)在R上单调递增,
∴f(x)的递增区间是(-∞,+∞).
(2)由f(x)是奇函数,得f(0)=0,∴a-
=a-1=0,∴a=1.
∴f(x)=1-
∵ex>0,∴ex+1>1,∴
∈(0,1),∴-
∈(-2,0),∴1-
∈(-1,1),
∴f(x)的值域是(-1,1)
f′(x)=-
| 0-2ex |
| (ex+1)2 |
| 2ex |
| (ex+1)2 |
∴f(x)的递增区间是(-∞,+∞).
(2)由f(x)是奇函数,得f(0)=0,∴a-
| 2 |
| e0+1 |
∴f(x)=1-
| 2 |
| ex+1 |
∵ex>0,∴ex+1>1,∴
| 1 |
| ex+1 |
| 2 |
| ex+1 |
| 2 |
| ex+1 |
∴f(x)的值域是(-1,1)
点评:本题考查函数的性质、单调性的判断及函数值域的求解,考查学生解决问题的能力.

练习册系列答案
相关题目
已知D是△ABC的边BC上(不包括B、C点)的一动点,且满足
=m
+n
,则
+
的最小值为( )
| AD |
| AB |
| AC |
| 1 |
| m |
| 2 |
| n |
| A、3 | ||
B、3+2
| ||
| C、4 | ||
D、4+2
|
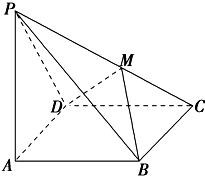 如图所示,在四棱锥P-ABCD中,PA⊥底面ABCD,且底面各边都相等,∠DAB=60°,PA=AD=2,M是PC上的一动点.
如图所示,在四棱锥P-ABCD中,PA⊥底面ABCD,且底面各边都相等,∠DAB=60°,PA=AD=2,M是PC上的一动点.