题目内容
在△ABC中，若a=3，b=
，∠A=
，求
（1）∠B的大小；
（2）△ABC的面积．
| 3 |
| π |
| 3 |
（1）∠B的大小；
（2）△ABC的面积．
考点：正弦定理
专题：解三角形
分析：（1）直接利用正弦定理推出B的正弦函数值，然后求出∠B的大小；
（2）求出C，然后利用三角形的面积公式求解△ABC的面积．
（2）求出C，然后利用三角形的面积公式求解△ABC的面积．
解答：
解：（1）在△ABC中，由正弦定理可知
=
，
即sinB=
=
=
．
又∵a＞b，
∴∠B=
．
（2）∴∠C=π-∠A-∠B=
．
s=
absinC=
×3×
=
．
| a |
| sinA |
| b |
| sinB |
即sinB=
| bsinA |
| a |
| ||||||
| 3 |
| 1 |
| 2 |
又∵a＞b，
∴∠B=
| π |
| 6 |
（2）∴∠C=π-∠A-∠B=
| π |
| 2 |
s=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
3
| ||
| 2 |
点评：本题考查三角形的解法，正弦定理的应用，注意角的大小与范围的判断是解题的关键，也是易错点．
练习册系列答案
相关题目
下列三角函数：①sin（kπ+
）②cos（2kπ+
）③sin（kπ+
）④cos[（2k+1）π-
]⑤sin[（2k+1）π-
]（k∈z）其中函数值与sin
的值相同的是（ ）
| 4π |
| 3 |
| π |
| 6 |
| π |
| 3 |
| π |
| 6 |
| π |
| 3 |
| π |
| 3 |
| A、②③④ | B、①⑤ | C、②⑤ | D、③⑤ |
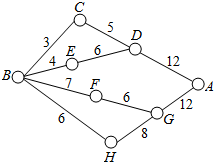如图，小圆圈表示网络的结点，结点之间的连线表示它们有网相联．连线标注的数字表示该段网线单位时间内可以通过的最大信息量，现从结点B向结点A传递信息，信息可以分开沿不同的路线同时传递，则单位时间内传递的最大信息量为（ ）| A、26 | B、24 | C、20 | D、19 |
函数f（x）=
的定义域是（ ）
| 1 | ||
|
A、(
| ||
B、[
| ||
C、(-∞，
| ||
D、(-∞，
|