题目内容
已知函数f（x）=
，若f[f（0）]=8c，则c= ．
|
考点：函数的值
专题：函数的性质及应用
分析：由已知得f（0）=2，从而f[f（0）]=f（2）=4+4c=8c，由此能求出c=1．
解答：
解：∵函数f（x）=
，f[f（0）]=8c，
∴f（0）=2，
f[f（0）]=f（2）=4+4c=8c，
解得c=1．
故答案为：1．
|
∴f（0）=2，
f[f（0）]=f（2）=4+4c=8c，
解得c=1．
故答案为：1．
点评：本题考查函数值的求法，是基础题，解题时要认真审题，注意函数性质的合理运用．
练习册系列答案
通城学典默写能手系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
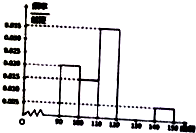某校高三数学竞赛初赛考试后，对考生的成绩进行统计（考生成绩均不低于90分，满分为150分），将成绩按如下方式分成六组，第一组[90，100）、第二组[100，110）…，第六组[140，150]，如图为其频率分布直方图的一部分，若第四、五、六组的人数依次成等差数列，且第六组有4人．
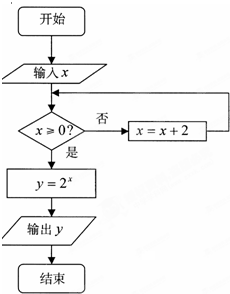如图所示的算法流程图中（注：“x=x+2”也可写成“x：=x+2”，均表示赋值语句），若输入的x值为-3，则输出的y值是（ ）下列等式中错误的是（ ）
| A、sin（π+α）=-sinα |
| B、cos（π-α）=cosα |
| C、cos（2π-α）=cosα |
| D、sin（2π+α）=sinα |