题目内容
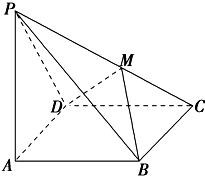 如图所示,在四棱锥P-ABCD中,PA⊥底面ABCD,且底面各边都相等,∠DAB=60°,PA=AD=2,M是PC上的一动点.
如图所示,在四棱锥P-ABCD中,PA⊥底面ABCD,且底面各边都相等,∠DAB=60°,PA=AD=2,M是PC上的一动点.(1)求四棱锥P-ABCD的体积
(2)当M满足什么条件时,平面MBD⊥平面PCD.证明你的结论.
考点:棱柱、棱锥、棱台的体积,平面与平面垂直的判定
专题:
分析:(1)利用棱锥的体积公式,直接求解四棱锥P-ABCD的体积
(2)当M满足满足DM⊥PC时,平面MBD⊥平面PCD.证明BD⊥PC,利用直线与平面垂直的判定定理,证明结论即可.
(2)当M满足满足DM⊥PC时,平面MBD⊥平面PCD.证明BD⊥PC,利用直线与平面垂直的判定定理,证明结论即可.
解答:
解:(1)解:v=
sh=
×
×4×2×2=
(2)证明:当PC上的点M满足DM⊥PC时,有PC⊥平面MBD,
证明如下:
连接AC与BD
底面ABCD各边都相等∴BD⊥AC.∵PA⊥底面ABCD∴PA⊥BD∴BD⊥面PAC∴BD⊥PC
当PC上的点M满足DM⊥PC时
有PC⊥平面MBD,
而PC?平面PCD,∴平面MBD⊥平面PCD.
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 4 |
4
| ||
| 3 |
(2)证明:当PC上的点M满足DM⊥PC时,有PC⊥平面MBD,
证明如下:
连接AC与BD
底面ABCD各边都相等∴BD⊥AC.∵PA⊥底面ABCD∴PA⊥BD∴BD⊥面PAC∴BD⊥PC
当PC上的点M满足DM⊥PC时
有PC⊥平面MBD,
而PC?平面PCD,∴平面MBD⊥平面PCD.

点评:本题考查棱锥的体积的求法,直线与平面垂直的判定定理的应用,考查空间想象能力以及计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列等式中错误的是( )
| A、sin(π+α)=-sinα |
| B、cos(π-α)=cosα |
| C、cos(2π-α)=cosα |
| D、sin(2π+α)=sinα |
函数f(x)=
的定义域是( )
| 1 | ||
|
A、(
| ||
B、[
| ||
C、(-∞,
| ||
D、(-∞,
|
已知集合A={x|0≤x≤2},B={y|1<y<3},则A∩B=( )
| A、[1,2) |
| B、[0,3) |
| C、(1,2] |
| D、[0,3] |
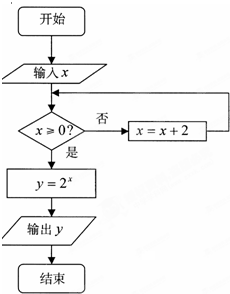 如图所示的算法流程图中(注:“x=x+2”也可写成“x:=x+2”,均表示赋值语句),若输入的x值为-3,则输出的y值是( )
如图所示的算法流程图中(注:“x=x+2”也可写成“x:=x+2”,均表示赋值语句),若输入的x值为-3,则输出的y值是( )