题目内容
已知D是△ABC的边BC上(不包括B、C点)的一动点,且满足
=m
+n
,则
+
的最小值为( )
| AD |
| AB |
| AC |
| 1 |
| m |
| 2 |
| n |
| A、3 | ||
B、3+2
| ||
| C、4 | ||
D、4+2
|
考点:基本不等式
专题:不等式的解法及应用
分析:利用向量共线定理、基本不等式的性质即可得出.
解答:
解:∵B,C,D三点共线,满足
=m
+n
,
∴m+n=1,m,n>0.
∴
+
=(m+n)(
+
)=3=
+
≥3+2
=3+2
,当且仅当n=
m=2-
.
∴
+
的最小值为3+2
.
故选:B.
| AD |
| AB |
| AC |
∴m+n=1,m,n>0.
∴
| 1 |
| m |
| 2 |
| n |
| 1 |
| m |
| 2 |
| n |
| n |
| m |
| 2m |
| n |
|
| 2 |
| 2 |
| 2 |
∴
| 1 |
| m |
| 2 |
| n |
| 2 |
故选:B.
点评:本题考查了向量共线定理、基本不等式的性质,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知单位向量
、
的夹角为60°,则|
+
|的值为( )
| a |
| b |
| a |
| b |
| A、3 | ||
| B、2 | ||
C、
| ||
D、
|
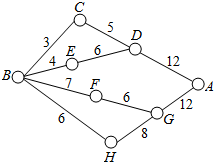 如图,小圆圈表示网络的结点,结点之间的连线表示它们有网相联.连线标注的数字表示该段网线单位时间内可以通过的最大信息量,现从结点B向结点A传递信息,信息可以分开沿不同的路线同时传递,则单位时间内传递的最大信息量为( )
如图,小圆圈表示网络的结点,结点之间的连线表示它们有网相联.连线标注的数字表示该段网线单位时间内可以通过的最大信息量,现从结点B向结点A传递信息,信息可以分开沿不同的路线同时传递,则单位时间内传递的最大信息量为( )| A、26 | B、24 | C、20 | D、19 |
已知集合A={x|0≤x≤2},B={y|1<y<3},则A∩B=( )
| A、[1,2) |
| B、[0,3) |
| C、(1,2] |
| D、[0,3] |
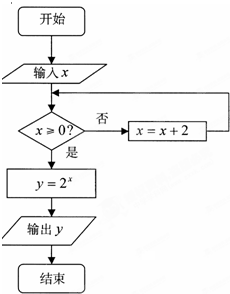 如图所示的算法流程图中(注:“x=x+2”也可写成“x:=x+2”,均表示赋值语句),若输入的x值为-3,则输出的y值是( )
如图所示的算法流程图中(注:“x=x+2”也可写成“x:=x+2”,均表示赋值语句),若输入的x值为-3,则输出的y值是( )