题目内容
2.双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的左、右焦点分别为F1、F2,P为双曲线右支上一点,且$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}=0$,若$∠P{F_1}{F_2}∈[{\frac{π}{12},\frac{π}{6}}]$,则双曲线离心率的取值范围是( )| A. | $[{2,\sqrt{3}+1}]$ | B. | $[{2,2\sqrt{3}+1}]$ | C. | $[{\sqrt{2},2}]$ | D. | $[{\sqrt{2},\sqrt{3}+1}]$ |
分析 设|PF1|=x,|PF2|=y,设∠PF1F2=θ,分析可得y-x=2a,tanθ=$\frac{x}{y}$,根据条件判断PF1⊥PF2,由双曲线的离心率公式可得e2=$\frac{{c}^{2}}{{a}^{2}}$=$\frac{4{c}^{2}}{4{a}^{2}}$=$\frac{{x}^{2}+{y}^{2}}{(y-x)^{2}}$=$\frac{{x}^{2}+{y}^{2}}{{x}^{2}+{y}^{2}-2xy}$=1+$\frac{2xy}{{x}^{2}+{y}^{2}-2xy}$=1+$\frac{2}{\frac{x}{y}+\frac{y}{x}-2}$=1+$\frac{2}{tanθ+\frac{1}{tanθ}-2}$,令t=tanθ+$\frac{1}{tanθ}$,分析tanθ的范围,由对号函数的性质分析可得t的范围,将t的范围代入其中,计算可得e2的范围,化简即可得答案.
解答 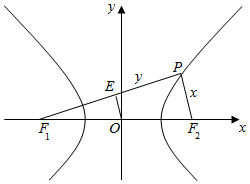 解:根据题意,设|PF1|=x,|PF2|=y,设∠PF1F2=θ,
解:根据题意,设|PF1|=x,|PF2|=y,设∠PF1F2=θ,
则有y-x=2a,tanθ=$\frac{x}{y}$,
又由$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}=0$,则有x2+y2=|F1F2|=4c2,
e2=$\frac{{c}^{2}}{{a}^{2}}$=$\frac{4{c}^{2}}{4{a}^{2}}$=$\frac{{x}^{2}+{y}^{2}}{(y-x)^{2}}$=$\frac{{x}^{2}+{y}^{2}}{{x}^{2}+{y}^{2}-2xy}$=1+$\frac{2xy}{{x}^{2}+{y}^{2}-2xy}$
=1+$\frac{2}{\frac{x}{y}+\frac{y}{x}-2}$=1+$\frac{2}{tanθ+\frac{1}{tanθ}-2}$,
令t=tanθ+$\frac{1}{tanθ}$,由于θ=$∠P{F_1}{F_2}∈[{\frac{π}{12},\frac{π}{6}}]$,
则tanθ∈(2-$\sqrt{3}$,$\frac{\sqrt{3}}{3}$),则t∈($\frac{4\sqrt{3}}{3}$,4),
则有2≤e2≤2$\sqrt{3}$+4,
则有$\sqrt{2}$≤e≤$\sqrt{3}$+1,
即双曲线离心率e的取值范围是[$\sqrt{2}$,$\sqrt{3}$+1];
故选:D.
点评 本题考查双曲线的几何性质,关键是根据条件判断PF1⊥PF2,结合正弦定理以及转化为函数最值问题.

| A. | {x|1≤x≤2} | B. | (1,2) | C. | {1,2} | D. | ∅ |
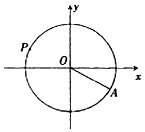 水车在古代是进行灌溉引水的工具,是人类的一项古老的发明,也是人类利用自然和改造自然的象征.如图是一个半径为R的水车,一个水斗从点A(3$\sqrt{3}$,-3)出发,沿圆周按逆时针方向匀速旋转,且旋转一周用时60秒.经过t秒后,水斗旋转到P点,设P的坐标为(x,y),其纵坐标满足y=f(t)=Rsin(ωt+φ)(t≥0,ω>0,|φ|<$\frac{π}{2}}$).则下列叙述错误的是( )
水车在古代是进行灌溉引水的工具,是人类的一项古老的发明,也是人类利用自然和改造自然的象征.如图是一个半径为R的水车,一个水斗从点A(3$\sqrt{3}$,-3)出发,沿圆周按逆时针方向匀速旋转,且旋转一周用时60秒.经过t秒后,水斗旋转到P点,设P的坐标为(x,y),其纵坐标满足y=f(t)=Rsin(ωt+φ)(t≥0,ω>0,|φ|<$\frac{π}{2}}$).则下列叙述错误的是( )| A. | $R=6,ω=\frac{π}{30},φ=-\frac{π}{6}$ | |
| B. | 当t∈[35,55]时,点P到x轴的距离的最大值为6 | |
| C. | 当t∈[10,25]时,函数y=f(t)单调递减 | |
| D. | 当t=20时,$|{PA}|=6\sqrt{3}$ |
| A. | (-∞,0)∪(0,$\frac{1}{2}$) | B. | (-∞,$\frac{1}{2}$) | C. | ($\frac{1}{2}$,+∞) | D. | (0,$\frac{1}{2}$) |
| A. | 32 | B. | 64 | C. | 128 | D. | 256 |
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{4}{5}$ | D. | 1 |
| A. | $[{\frac{π}{12},\frac{π}{4}}]$ | B. | $[{\frac{π}{6},\frac{5π}{12}})$ | C. | $[{\frac{π}{6},\frac{π}{3}}]$ | D. | $({\frac{π}{6},\frac{π}{4}}]$ |
| A. | [0,+∞) | B. | (1,+∞) | C. | [0,1) | D. | (0,+∞) |