题目内容
12.已知集合A={x|x>1},B={y|y=x2,x∈R},则A∩B=( )| A. | [0,+∞) | B. | (1,+∞) | C. | [0,1) | D. | (0,+∞) |
分析 运用二次函数的性质,化简集合B,再根据集合交集的定义,即可得到所求.
解答 解:集合A={x|x>1},
B={y|y=x2,x∈R}={y|y≥0},
则A∩B={m|m>1}=(1,+∞).
故选:B.
点评 本题考查集合的交集的运算,注意运用二次函数的性质和交集的定义,考查运算能力,属于基础题.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
2.双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的左、右焦点分别为F1、F2,P为双曲线右支上一点,且$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}=0$,若$∠P{F_1}{F_2}∈[{\frac{π}{12},\frac{π}{6}}]$,则双曲线离心率的取值范围是( )
| A. | $[{2,\sqrt{3}+1}]$ | B. | $[{2,2\sqrt{3}+1}]$ | C. | $[{\sqrt{2},2}]$ | D. | $[{\sqrt{2},\sqrt{3}+1}]$ |
7.在△ABC所在平面上有一点P,满足$\overrightarrow{PA}+\overrightarrow{PB}+\overrightarrow{PC}=\overrightarrow{BC}$,$\overrightarrow{PC}=x\overrightarrow{AB}+y\overrightarrow{AC}$,则x+y=( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $-\frac{1}{3}$ | D. | $-\frac{1}{2}$ |
17.设m、n是两条不同的直线,α、β是两个不同的平面,则m⊥β的一个充分条件是( )
| A. | α⊥β且m?α | B. | m∥n且n⊥β | C. | α⊥β且m∥α | D. | m⊥n且n∥β |
1.已知集合A={0,2,4},B={x|3x-x2≥0},则集合A∩B的子集个数为( )
| A. | 2 | B. | 3 | C. | 4 | D. | 8 |
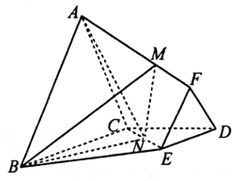 如图,在棱台ABC-FED中,△DEF与△ABC分别是棱长为1与2的正三角形,平面ABC⊥平面BCDE,四边形BCDE为直角梯形,BC⊥CD,CD=1,N为CE中点,$\overrightarrow{AM}=λ\overrightarrow{AF}({λ∈R,λ>0})$.
如图,在棱台ABC-FED中,△DEF与△ABC分别是棱长为1与2的正三角形,平面ABC⊥平面BCDE,四边形BCDE为直角梯形,BC⊥CD,CD=1,N为CE中点,$\overrightarrow{AM}=λ\overrightarrow{AF}({λ∈R,λ>0})$. 18、甲、乙两位同学参加数学文化知识竞赛培训,现分别从他们在培训期间参加的若干次测试成绩中随机抽取8次,记录如下:
18、甲、乙两位同学参加数学文化知识竞赛培训,现分别从他们在培训期间参加的若干次测试成绩中随机抽取8次,记录如下: