题目内容
12.设双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点F,过点F作与x轴垂直的直线l交两渐近线于A,B两点,且与双曲线在第一象限的交点为P,设O为坐标原点,若$\overrightarrow{OP}$=λ$\overrightarrow{OA}$+μ$\overrightarrow{OB}$(λ,μ∈R),λμ=$\frac{1}{16}$,则该双曲线的离心率为( )| A. | $\frac{3\sqrt{2}}{2}$ | B. | $\frac{3\sqrt{5}}{5}$ | C. | 3 | D. | 2 |
分析 由方程可得渐近线,可得A,B,P的坐标,由已知向量式可得λ+μ=1,λ-μ=$\frac{b}{c}$,解之可得λμ的值,由λμ=$\frac{1}{16}$,可得a,c的关系,由离心率的定义可得.
解答 解:双曲线的渐近线为:y=±$\frac{b}{a}$x,设焦点F(c,0),则
A(c,$\frac{bc}{a}$),B(c,-$\frac{bc}{a}$),P(c,$\frac{{b}^{2}}{a}$),
因为$\overrightarrow{OP}$=λ$\overrightarrow{OA}$+μ$\overrightarrow{OB}$,
所以(c,$\frac{{b}^{2}}{a}$)=((λ+μ)c,(λ-μ)$\frac{bc}{a}$),
所以λ+μ=1,λ-μ=$\frac{b}{c}$,
解得:λ=$\frac{c+b}{2c}$,μ=$\frac{c-b}{2c}$,
又由λμ=$\frac{1}{16}$,得:$\frac{{c}^{2}-{b}^{2}}{4{c}^{2}}=\frac{1}{16}$,
解得$\frac{{a}^{2}}{{c}^{2}}$=$\frac{1}{4}$,
所以,e=2.
故选:D
点评 本题考查双曲线的简单性质,涉及双曲线的离心率的求解,属中档题.

练习册系列答案
相关题目
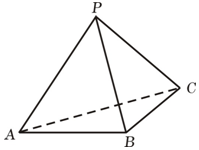 如图,三棱锥P-ABC中,△ABC为等腰直角三角形,AB=BC=2,PA=PB=PC=$\sqrt{6}$.
如图,三棱锥P-ABC中,△ABC为等腰直角三角形,AB=BC=2,PA=PB=PC=$\sqrt{6}$.