题目内容
4.已知原命题“若a>b>0,则$\frac{1}{a}$<$\frac{1}{b}$”,则原命题,逆命题,否命题,逆否命题中真命题个数为( )| A. | 0 | B. | 1 | C. | 2 | D. | 4 |
分析 根据逆否命题的等价性分别进行判断即可.
解答 解:若a>b>0,则$\frac{1}{a}$<$\frac{1}{b}$成立,则原命题为真命题,则逆否命题为真命题,
命题的逆命题为若$\frac{1}{a}$<$\frac{1}{b}$,则a>b>0,为假命题,当a<0,b>0时,结论就不成立,则逆命题为假命题,否命题也为假命题,
故真命题的个数为2个,
故选:C
点评 本题主要考查四种命题的关系,根据逆否命题的等价性只需要判断两个命题的真假即可.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
12.设双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点F,过点F作与x轴垂直的直线l交两渐近线于A,B两点,且与双曲线在第一象限的交点为P,设O为坐标原点,若$\overrightarrow{OP}$=λ$\overrightarrow{OA}$+μ$\overrightarrow{OB}$(λ,μ∈R),λμ=$\frac{1}{16}$,则该双曲线的离心率为( )
| A. | $\frac{3\sqrt{2}}{2}$ | B. | $\frac{3\sqrt{5}}{5}$ | C. | 3 | D. | 2 |
16.已知函数f(x)=$\frac{x}{{e}^{x}}$,则f′(x)=( )
| A. | $\frac{x-1}{{e}^{x}}$ | B. | $\frac{x+1}{{e}^{x}}$ | C. | $\frac{-x-1}{{e}^{x}}$ | D. | $\frac{1-x}{{e}^{x}}$ |
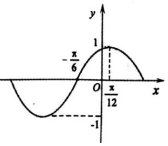 函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,将y=f(x)的图象向右平移$\frac{π}{4}$个单位长度后得到函数y=g(x)的图象.
函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,将y=f(x)的图象向右平移$\frac{π}{4}$个单位长度后得到函数y=g(x)的图象.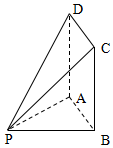 如图,四边形ABCD为矩形,PB=20,BC=30,PA⊥平面ABCD.
如图,四边形ABCD为矩形,PB=20,BC=30,PA⊥平面ABCD.