题目内容
数列{an}的前n项和为Sn,对n∈N*,点(n,an)横在直线f(x)=-2x+k上,点(n,Sn)恒在抛物线g(x)=ax2+x上,其中k,a为常数.
(1)求数列{an}的通项公式;
(2)求直线f(x)与抛物线g(x)所围成的封闭图形的面积.
(1)求数列{an}的通项公式;
(2)求直线f(x)与抛物线g(x)所围成的封闭图形的面积.
考点:数列与函数的综合,定积分
专题:计算题,函数的性质及应用,点列、递归数列与数学归纳法
分析:(1)由题意得,an=k-2n,Sn=an2+n,由a1=S1,an=Sn-Sn-1即可求出a=-1,k=2;
(2)由于f(x)=2-2x,g(x)=x-x2,画出直线和抛物线,求得交点A(1,0),B(2,-2),运用定积分求出曲线AB和直线x=2和x轴围成的面积,再运用三角形ABC的面积减去它,即可得到所求面积.
(2)由于f(x)=2-2x,g(x)=x-x2,画出直线和抛物线,求得交点A(1,0),B(2,-2),运用定积分求出曲线AB和直线x=2和x轴围成的面积,再运用三角形ABC的面积减去它,即可得到所求面积.
解答:
 解:(1)点(n,an)恒在直线f(x)=-2x+k上,则有an=k-2n,
解:(1)点(n,an)恒在直线f(x)=-2x+k上,则有an=k-2n,
点(n,Sn)恒在抛物线g(x)=ax2+x上,则有Sn=an2+n,
则a1=S1=k-2=a+1,an=Sn-Sn-1=an2+n-a(n-1)2-(n-1)
=2an+1-a,则有a=-1,k=2,
即有an=2-2n;
(2)由于an=2-2n,Sn=n-n2.
则f(x)=2-2x,g(x)=x-x2,
如图画出直线和抛物线,求得交点A(1,0),B(2,-2),
曲线AB和直线x=2和x轴围成的面积为|
(x-x2)dx|=|(
x2-
x3)|
|
=|(2-
)-(
-
)|=
,
三角形ABC的面积为
×2×1=1,
则直线f(x)与抛物线g(x)所围成的封闭图形的面积为1-
=
.
 解:(1)点(n,an)恒在直线f(x)=-2x+k上,则有an=k-2n,
解:(1)点(n,an)恒在直线f(x)=-2x+k上,则有an=k-2n,点(n,Sn)恒在抛物线g(x)=ax2+x上,则有Sn=an2+n,
则a1=S1=k-2=a+1,an=Sn-Sn-1=an2+n-a(n-1)2-(n-1)
=2an+1-a,则有a=-1,k=2,
即有an=2-2n;
(2)由于an=2-2n,Sn=n-n2.
则f(x)=2-2x,g(x)=x-x2,
如图画出直线和抛物线,求得交点A(1,0),B(2,-2),
曲线AB和直线x=2和x轴围成的面积为|
| ∫ | 2 1 |
| 1 |
| 2 |
| 1 |
| 3 |
2 1 |
=|(2-
| 8 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 5 |
| 6 |
三角形ABC的面积为
| 1 |
| 2 |
则直线f(x)与抛物线g(x)所围成的封闭图形的面积为1-
| 5 |
| 6 |
| 1 |
| 6 |
点评:本题考查数列的通项和求和,及其之间的关系,考查封闭图形的面积求法,注意运用定积分的方法,考查运算能力,属于中档题.

练习册系列答案
相关题目
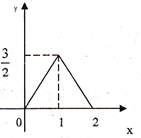
图中的图象所表示的函数的解析式为( )

A、y=
| ||
B、y=
| ||
C、y=
| ||
| D、2-|x-1|(0≤x≤2) |