题目内容
已知cosθ=
,求
的值.
| 4 |
| 5 |
| [sin(180°-θ)+cos(θ-360°)] |
| cot(270°-θ) |
考点:运用诱导公式化简求值
专题:三角函数的求值
分析:由题意,可先求得sinθ=±
=±
,原式可化简为
=
=cosθ+
,从而代入即可求值.
| 1-cos2θ |
| 3 |
| 5 |
| [sin(180°-θ)+cos(θ-360°)] |
| cot(270°-θ) |
| sinθ+cosθ |
| tanθ |
| cos2θ |
| sinθ |
解答:
解:cosθ=
,则sinθ=±
=±
,
=
=cosθ+
=
±
=
±
.
故
的值为
或-
.
| 4 |
| 5 |
| 1-cos2θ |
| 3 |
| 5 |
| [sin(180°-θ)+cos(θ-360°)] |
| cot(270°-θ) |
| sinθ+cosθ |
| tanθ |
| cos2θ |
| sinθ |
| 4 |
| 5 |
| ||
|
| 4 |
| 5 |
| 16 |
| 15 |
故
| [sin(180°-θ)+cos(θ-360°)] |
| cot(270°-θ) |
| 28 |
| 15 |
| 4 |
| 15 |
点评:本题主要考查同角三角函数的基本关系、诱导公式的应用,属于中档题.

练习册系列答案
相关题目
设f(x)为定义在R上的奇函数,当x≥0时,f(x)=2x+2x+b(b为常数),则f(-1)=( )
| A、3 | B、1 | C、-1 | D、-3 |
已知等比数列{an}的前n项积为Πn,若a2•a4•a6=8,则Π7等于( )
| A、512 | B、256 |
| C、81 | D、128 |
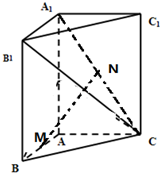 如图,已知三棱柱ABC-A1B1C1,侧面BCC1B1⊥底面ABC.
如图,已知三棱柱ABC-A1B1C1,侧面BCC1B1⊥底面ABC.