题目内容
已知定义在R上的函数f(x)=D(x)-|x2-2|,其中D(x)=
,用列举法写出f(x)所有零点组成的集合.
|
考点:函数的零点
专题:计算题,函数的性质及应用,集合
分析:令f(x)=0,讨论当x∈Q,当x∉Q,解方程即可得到零点,注意运用列举法表示集合.
解答:
解:令f(x)=0,
则当x∈Q,1-|x2-2|=0,解得,x=±
或±1,则有x=±1;
当x∉Q,|x2-2|=0,解得,x=±
,
则f(x)所有零点组成的集合为{-1,1,
,-
}.
则当x∈Q,1-|x2-2|=0,解得,x=±
| 3 |
当x∉Q,|x2-2|=0,解得,x=±
| 2 |
则f(x)所有零点组成的集合为{-1,1,
| 2 |
| 2 |
点评:本题考查函数的零点的求法,考查集合的表示方法,考查运算能力,属于基础题.

练习册系列答案
相关题目
已知等比数列{an}的前n项积为Πn,若a2•a4•a6=8,则Π7等于( )
| A、512 | B、256 |
| C、81 | D、128 |
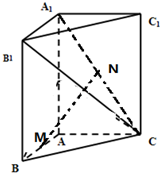 如图,已知三棱柱ABC-A1B1C1,侧面BCC1B1⊥底面ABC.
如图,已知三棱柱ABC-A1B1C1,侧面BCC1B1⊥底面ABC.