题目内容
19.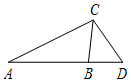 在△ABC中,角A、B、C所对的边分别是a、b、c,已知$\sqrt{3}a=2csinA$且c<b.
在△ABC中,角A、B、C所对的边分别是a、b、c,已知$\sqrt{3}a=2csinA$且c<b. (Ⅰ)求角C的大小;
(Ⅱ)若b=4,延长AB至D,使BC=BD,且AD=5,求△ACD的面积.
分析 (Ⅰ)由正弦定理化$\sqrt{3}a=2csinA$,即可求出sinC的值,从而求出C;
(Ⅱ)根据图形设BC=x,利用余弦定理求出x的值,再求出AB的值,
利用正弦定理求出sinA,再计算△ACD的面积.
解答 解:(Ⅰ)△ABC中,$\sqrt{3}a=2csinA$,
由正弦定理得,$\sqrt{3}sinA=2sinCsinA$,
∴$sinC=\frac{{\sqrt{3}}}{2}$,
又c<b,∴$C=\frac{π}{3}$; …(6分)
(Ⅱ)如图所示,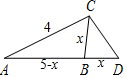
设BC=x,则AB=5-x,
在△ABC中,由余弦定理得
$(5-x{)^2}={x^2}+{4^2}-2•x•4cos\frac{π}{3}$,
求得$x=\frac{3}{2}$,即$BC=\frac{3}{2}$,
所以$AB=\frac{7}{2}$,…(8分)
在△ABC中,由正弦定理得$\frac{BC}{sinA}=\frac{AB}{sinC}$,
∴$sinA=\frac{BCsinC}{AB}=\frac{{3\sqrt{3}}}{14}$,…(10分)
∴△ACD的面积为
$S=\frac{1}{2}AC•AD•sinA$=$\frac{1}{2}×4×5×\frac{{3\sqrt{3}}}{14}=\frac{{15\sqrt{3}}}{7}$.…(12分)
点评 本题考查了正弦、余弦定理的应用问题,是基础题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
10.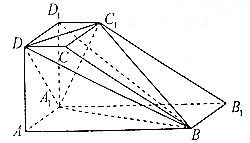 如图,直四棱柱ABCD-A1B1C1D1的底面ABCD是直角梯形,其中AB⊥AD,AB=2AD=2AA1=4,CD=1.
如图,直四棱柱ABCD-A1B1C1D1的底面ABCD是直角梯形,其中AB⊥AD,AB=2AD=2AA1=4,CD=1.
(Ⅰ)证明:BD1⊥平面A1C1D;
(Ⅱ)求多面体BDC1A1D1的体积.
 如图,直四棱柱ABCD-A1B1C1D1的底面ABCD是直角梯形,其中AB⊥AD,AB=2AD=2AA1=4,CD=1.
如图,直四棱柱ABCD-A1B1C1D1的底面ABCD是直角梯形,其中AB⊥AD,AB=2AD=2AA1=4,CD=1.(Ⅰ)证明:BD1⊥平面A1C1D;
(Ⅱ)求多面体BDC1A1D1的体积.
14.设F1,F2是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的两个焦点,若点P在双曲线上,且∠F1PF2=90°,|PF1|•|PF2|=2,则b=( )
| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | $2\sqrt{2}$ |
4.已知曲线C:y=ex和直线l:ax+by=0,若直线l上有且只有两个关于y轴的对称点在曲线C上,则$\frac{b}{a}$的取值范围是( )
| A. | (-∞,-e) | B. | (-∞,$\frac{1}{e}$) | C. | (0,$\frac{1}{e}$) | D. | (e,+∞) |
11.已知F1、F2为双曲线的焦点,过F2垂直于实轴的直线交双曲线于A、B两点,BF1交y轴于点C,若AC⊥BF1,则双曲线的离心率为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2$\sqrt{2}$ | D. | 2$\sqrt{3}$ |