题目内容
4.已知曲线C:y=ex和直线l:ax+by=0,若直线l上有且只有两个关于y轴的对称点在曲线C上,则$\frac{b}{a}$的取值范围是( )| A. | (-∞,-e) | B. | (-∞,$\frac{1}{e}$) | C. | (0,$\frac{1}{e}$) | D. | (e,+∞) |
分析 设k=-$\frac{a}{b}$,求出l关于y轴的对称直线方程,把直线l上有且只有两个点关于y轴的对称点在曲线Γ:y=ex上,转化为直线y=-kx与y=ex有两个交点,然后求出过原点与曲线Γ:y=ex相切的直线的斜率得答案.
解答 解:设k=-$\frac{a}{b}$,直线l:y=kx关于y轴的对称直线方程为y=-kx,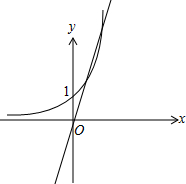
要使直线l上有且只有两个点关于y轴的对称点在曲线Γ:y=ex上,
则直线y=-kx与y=ex有两个交点,
如图,设过原点的直线切曲线y=ex于P(m,em),
由y=ex,得y′=ex,∴y′=em,
则切线方程为y-em=em(x-m),
把O(0,0)代入,可得m=1,
∴切线的斜率k=e1=e,
∴-k>e,则k<-e,
∴-$\frac{a}{b}$<-e,
∴$\frac{b}{a}$的取值范围是(0,$\frac{1}{e}$).
故选:C.
点评 本题考查利用导数研究过曲线上某点处的切线方程,考查数学转化思想方法,是中档题.

练习册系列答案
相关题目
14.某单位实行休年假制度三年以来,50名职工休年假的次数进行的调查统计结果如表所示:
根据表中信息解答以下问题:
(1)从该单位任选两名职工,求这两人休年假次数之和为4的概率;
(2)从该单位任选两名职工,用ξ表示这两人休年假次数之差的绝对值,求随机变量ξ的分布列及数学期望Eξ.
| 休假次数 | 0 | 1 | 2 | 3 |
| 人数 | 5 | 10 | 20 | 15 |
(1)从该单位任选两名职工,求这两人休年假次数之和为4的概率;
(2)从该单位任选两名职工,用ξ表示这两人休年假次数之差的绝对值,求随机变量ξ的分布列及数学期望Eξ.
15.某几何体的三视图如图所示,则该几何体的体积为( )
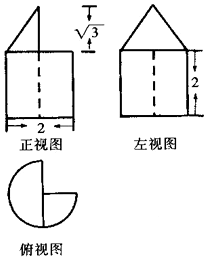

| A. | $\frac{9+\sqrt{3}}{6}$π | B. | $\frac{6+\sqrt{3}}{6}$π | C. | $\frac{3+\sqrt{3}}{6}$π | D. | $\frac{12+\sqrt{3}}{6}$π |
12.阅读如图的程序框图,运行相应的程序,输出的结果是( )


| A. | 3 | B. | $\frac{17}{7}$ | C. | $\frac{7}{3}$ | D. | $\frac{3}{7}$ |
9.设命题p:?x0∈(0,+∞),x0+$\frac{1}{{x}_{0}}$>3;命题q:?x∈(2,+∞),x2>2x,则下列命题为真的是( )
| A. | p∧(¬q) | B. | (¬p)∧q | C. | p∧q | D. | (¬p)∨q |
14.设函数$f(x)=\frac{{6sinxcosx-4cosx{{sin}^3}x}}{{2\sqrt{2}+sin(2x+\frac{π}{4})+cos(2x+\frac{π}{4})}}$,则( )
| A. | y=f(x)是偶函数,在$(0,\frac{π}{2})$上单调递增 | B. | y=f(x)是奇函数,在$(0,\frac{π}{4})$上单调递增 | ||
| C. | y=f(x)是偶函数,在$(0,\frac{π}{2})$上单调递减 | D. | y=f(x)是奇函数,在$(0,\frac{π}{4})$上单调递减 |
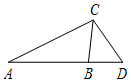 在△ABC中,角A、B、C所对的边分别是a、b、c,已知$\sqrt{3}a=2csinA$且c<b.
在△ABC中,角A、B、C所对的边分别是a、b、c,已知$\sqrt{3}a=2csinA$且c<b.