题目内容
某农家旅游公司有客房300间，每间日房租为20元，每天都客满．公司欲提高档次，并提高租金．如果每间日房租每增加1元，客房出租数就会减少5间．若不考虑其他因素，旅游公司将房间租金提高x元，每天客房的租金总收入y元．
（1）写出y与x之间的函数关系式；
（2）旅游公司将房间租金提高到多少元时，每天客房的租金总收入最高？
（1）写出y与x之间的函数关系式；
（2）旅游公司将房间租金提高到多少元时，每天客房的租金总收入最高？
考点：函数解析式的求解及常用方法,函数的最值及其几何意义
专题：应用题
分析：这是一道函数的实际应用题，（1）总收入=第间租金*租出房间数，
（2）y是关于x的二次函数利用配方法就可以求出最大值．
（2）y是关于x的二次函数利用配方法就可以求出最大值．
解答：
解：（1）由题知y=（20+x）（300-5x）
即y=-5x2+200x+6000（x∈[0，60]；
（2）∵y=-5（x-20）2+8000，∴x=20时ymax=8000
所以旅游公司将房间租金提高到40元时，每天客房的租金总收入最高．
即y=-5x2+200x+6000（x∈[0，60]；
（2）∵y=-5（x-20）2+8000，∴x=20时ymax=8000
所以旅游公司将房间租金提高到40元时，每天客房的租金总收入最高．
点评：函数的应用题，理解题意是关键，本题属于基础题．
练习册系列答案
相关题目
下列选项中，p是q的必要不充分条件的是（ ）
| A、p：x=1，q：x2=x |
| B、p：|a|＞|b|，g：a2＞b2 |
| C、p：x＞a2+b2，q：x＞2ab |
| D、p：a+c＞b+d，q：a＞b且c＞d |
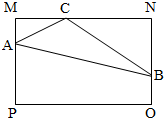如图，已知四边形MNOP是一个矩形，MN=