题目内容
已知函数f(x)=x3-3x2+2x
(Ⅰ)在p0处的切线平行于直线y=-x-1,求p0点的坐标;
(Ⅱ)求过原点的切线方程.
(Ⅰ)在p0处的切线平行于直线y=-x-1,求p0点的坐标;
(Ⅱ)求过原点的切线方程.
考点:利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(Ⅰ)求出原函数的导函数,得到函数在P0处的切线的斜率,由斜率等于-1求得P0点的坐标;
(Ⅱ)由(Ⅰ)可得函数f(x)过切点P0(x0,y0)的切线方程,代入原点坐标求得P0的坐标,进一步求出切线的斜率,由点斜式得切线方程.
(Ⅱ)由(Ⅰ)可得函数f(x)过切点P0(x0,y0)的切线方程,代入原点坐标求得P0的坐标,进一步求出切线的斜率,由点斜式得切线方程.
解答:
解:(Ⅰ)由f(x)=x3-3x2+2x,
得f′(x)=3x2-6x+2,
设P0(x0,y0),
则f′(x0)=3x02-6x0+2.
∵f(x)在P0处的切线平行于直线y=-x-1,
∴3x02-6x0+2=-1,
即(x0-1)2=0,x0=1.
∴f(x0)=f(1)=0.
即P0点的坐标为(1,0);
(Ⅱ)由(Ⅰ)知,函数f(x)过切点P0(x0,y0)的切线方程为:
y-x03+3x02-2x0=(3x02-6x0+2)(x-x0),
把(0,0)代入得:2x03-3x0=0.
解得x0=0或x0=
.
当x0=0时,斜率为2,切线方程为y=2x;
当x0=
时,切点为(
,-
),斜率为-
.
切线方程为y+
=-
(x-
),整理得,y=-
x.
∴过原点的切线方程为y=2x,y=-
x.
得f′(x)=3x2-6x+2,
设P0(x0,y0),
则f′(x0)=3x02-6x0+2.
∵f(x)在P0处的切线平行于直线y=-x-1,
∴3x02-6x0+2=-1,
即(x0-1)2=0,x0=1.
∴f(x0)=f(1)=0.
即P0点的坐标为(1,0);
(Ⅱ)由(Ⅰ)知,函数f(x)过切点P0(x0,y0)的切线方程为:
y-x03+3x02-2x0=(3x02-6x0+2)(x-x0),
把(0,0)代入得:2x03-3x0=0.
解得x0=0或x0=
| 3 |
| 2 |
当x0=0时,斜率为2,切线方程为y=2x;
当x0=
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 8 |
| 1 |
| 4 |
切线方程为y+
| 3 |
| 8 |
| 1 |
| 4 |
| 3 |
| 2 |
| 1 |
| 4 |
∴过原点的切线方程为y=2x,y=-
| 1 |
| 4 |
点评:本题考查利用导数研究曲线上某点处的切线方程,解答的关键在于区分给出的点是否为切点,该题是中档题,属易错题.

练习册系列答案
相关题目
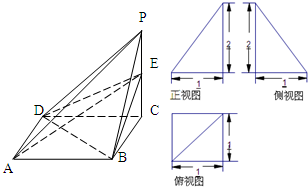 已知四棱锥P-ABCD的三视图和直观图如图所示,其中正视图、侧视图是直角三角形,俯视图是有一条对角线的正方形.E是侧棱PC上的动点.
已知四棱锥P-ABCD的三视图和直观图如图所示,其中正视图、侧视图是直角三角形,俯视图是有一条对角线的正方形.E是侧棱PC上的动点.