题目内容
已知圆C1:(x-1)2+(y-2)2=1
(1)求过点P(2,4)所作的圆C1的切线方程;
(2)若圆C1与圆C2:(x+1)2+(y-1)2=4相交于A、B两点,求线段AB的长度.
(1)求过点P(2,4)所作的圆C1的切线方程;
(2)若圆C1与圆C2:(x+1)2+(y-1)2=4相交于A、B两点,求线段AB的长度.
考点:圆的切线方程,圆与圆的位置关系及其判定
专题:直线与圆
分析:(1)当斜率存在时,用点斜式设切线方程,根据圆心到直线的距离等于半径,求得k的值,可得切线方程.当斜率不存在时,易得切线方程,从而得出结论.
(2)把两个圆的方程相减可得直线AB方程,求出圆心C1(1,2)到直线AB距离d,利用弦长公式求得|AB|的值
(2)把两个圆的方程相减可得直线AB方程,求出圆心C1(1,2)到直线AB距离d,利用弦长公式求得|AB|的值
解答:
解:(1)当斜率存在时,设切线方程为y-4=k(x-2)即kx-y+4-2k=0,
于是
=1,解得k=
,切线方程为3x-4y+10=0.
当斜率不存在时,得切线方程为x=2,
综上,切线方程为3x-4y+10=0或x=2.
(2)把两个圆的方程相减可得直线AB方程:2x+y-3=0,
则圆心C1(1,2)到直线AB距离d=
=
,
故|AB|=2
=
.
于是
| |k-2+4-2k| | ||
|
| 3 |
| 4 |
当斜率不存在时,得切线方程为x=2,
综上,切线方程为3x-4y+10=0或x=2.
(2)把两个圆的方程相减可得直线AB方程:2x+y-3=0,
则圆心C1(1,2)到直线AB距离d=
| |2+2-3| | ||
|
| ||
| 5 |
故|AB|=2
1-(
|
4
| ||
| 5 |
点评:本题主要考查用点斜式求直线的方程,求两个圆的公共弦所在的直线方程的方法,点到直线的距离公式、弦长公式的应用,体现了分类讨论的数学思想,属于中档题.

练习册系列答案
相关题目
 在三棱柱ABC-A1B1C1中,侧面ABB1A1为矩形,AB=1,AA1=
在三棱柱ABC-A1B1C1中,侧面ABB1A1为矩形,AB=1,AA1=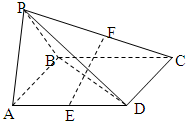 如图,四棱锥P-ABCD的底面是平行四边形,∠BAD=60°,平面PAB⊥平面ABCD,PA=PB=AB=
如图,四棱锥P-ABCD的底面是平行四边形,∠BAD=60°,平面PAB⊥平面ABCD,PA=PB=AB= 如图茎叶图记录了甲、乙两组各四名同学的植树棵数.乙组记录中有一个数据模糊,无法确认,在图中以X表示.
如图茎叶图记录了甲、乙两组各四名同学的植树棵数.乙组记录中有一个数据模糊,无法确认,在图中以X表示.