题目内容
给出下列命题:
①若a>b,则
<
②若不等式kx2-kx-1<0的解集为R,则-4<k<0
③若ac2>bc2,则a>b
④若c>a>b>0,则
>
,
⑤函数y=
+
的最小值是2
其中正确的命题序号是 .
①若a>b,则
| 1 |
| a |
| 1 |
| b |
②若不等式kx2-kx-1<0的解集为R,则-4<k<0
③若ac2>bc2,则a>b
④若c>a>b>0,则
| a |
| c-a |
| b |
| c-b |
⑤函数y=
| x2+4 |
| 3 | ||
|
| 3 |
其中正确的命题序号是
考点:基本不等式
专题:不等式的解法及应用
分析:①取a=2,b=-1,即可判断出;
②由于k=0也满足条件即可判断出;
③由于ac2>bc2,可得c2>0,利用不等式的基本性质即可得出;
④利用作差法和不等式的基本性质即可判断出;
⑤利用基本不等式的性质及其等号成立的条件即可判断出.
②由于k=0也满足条件即可判断出;
③由于ac2>bc2,可得c2>0,利用不等式的基本性质即可得出;
④利用作差法和不等式的基本性质即可判断出;
⑤利用基本不等式的性质及其等号成立的条件即可判断出.
解答:
解:①若a>b,取a=2,b=-1,则
<
不成立,故不正确;
②若不等式kx2-kx-1<0的解集为R,则-4<k<0不正确,k=0也满足条件,因此不正确;
③若ac2>bc2,则c2>0,∴a>b,正确;
④若c>a>b>0,则a(c-b)-b(c-a)=c(a-b)>0,∴
>
,正确;
⑤函数y=
+
≥2
=2
,当且仅当x2=-1时取等号,此方程无解,因此y>2
,其最小值大于2
,因此不正确.
综上可知:只有③④正确.
故答案为:③④.
| 1 |
| a |
| 1 |
| b |
②若不等式kx2-kx-1<0的解集为R,则-4<k<0不正确,k=0也满足条件,因此不正确;
③若ac2>bc2,则c2>0,∴a>b,正确;
④若c>a>b>0,则a(c-b)-b(c-a)=c(a-b)>0,∴
| a |
| c-a |
| b |
| c-b |
⑤函数y=
| x2+4 |
| 3 | ||
|
|
| 3 |
| 3 |
| 3 |
综上可知:只有③④正确.
故答案为:③④.
点评:本题考查了不等式的基本性质和基本不等式的性质,属于中档题.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
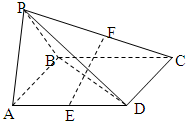 如图,四棱锥P-ABCD的底面是平行四边形,∠BAD=60°,平面PAB⊥平面ABCD,PA=PB=AB=
如图,四棱锥P-ABCD的底面是平行四边形,∠BAD=60°,平面PAB⊥平面ABCD,PA=PB=AB= 如图茎叶图记录了甲、乙两组各四名同学的植树棵数.乙组记录中有一个数据模糊,无法确认,在图中以X表示.
如图茎叶图记录了甲、乙两组各四名同学的植树棵数.乙组记录中有一个数据模糊,无法确认,在图中以X表示.