题目内容
已知正实数x，y满足lnx+lny=0，且x＞2y，若k（x-2y）≤x2+4y2恒成立，则k的取值范围是 ．
考点：函数恒成立问题
专题：不等式的解法及应用
分析：由已知得到xy=1，结合x＞2y把不等式k（x-2y）≤x2+4y2化为k≤(x-2y)+
，利用基本不等式求其最小值后得答案．
| 4 |
| x-2y |
解答：
解：由lnx+lny=0，得xy=1，
又x＞2y，
∴x-2y＞0，
不等式k（x-2y）≤x2+4y2恒成立，
即k≤
=
=(x-2y)+
．
令t=(x-2y)+
，
则t≥2
=4．
当且仅当
，即x=
+1，y=
时上式等号成立．
∴k≤4．
故答案为：k≤4．
又x＞2y，
∴x-2y＞0，
不等式k（x-2y）≤x2+4y2恒成立，
即k≤
| x2+4y2 |
| x-2y |
| (x-2y)2+4 |
| x-2y |
| 4 |
| x-2y |
令t=(x-2y)+
| 4 |
| x-2y |
则t≥2
(x-2y)•
|
当且仅当
|
| 3 |
| ||
| 2 |
∴k≤4．
故答案为：k≤4．
点评：本题考查了函数恒成立问题，考查了对数的运算性质，训练了利用基本不等式求最值，是中档题．
练习册系列答案
相关题目
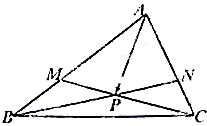在△ABC中，点M、N分别在边AB、AC上，且| AM |
| MB |
| AN |
| 3 |
| 5 |
| AC |
| AB |
| a |
| AC |
| b |
| AP |
| a |
| b |
A、
| ||||||||||
B、
| ||||||||||
C、
| ||||||||||
D、
|