题目内容
一家公司计划生产某种小型产品的月固定成本为1万元,每生产1万件需要再投入2万元,设该公司一个月内生产该小型产品x万件并全部销售完,每万件的销售收入为4-x万元,且每万件国家给予补助2e-
-
万元.(e为自然对数的底数,e是一个常数)
(Ⅰ)写出月利润f(x)(万元)关于月产量x(万件)的函数解析式
(Ⅱ)当月产量在[1,2e]万件时,求该公司在生产这种小型产品中所获得的月利润最大值(万元)及此时的月生成量值(万件).(注:月利润=月销售收入+月国家补助-月总成本)
| 2elnx |
| x |
| 1 |
| x |
(Ⅰ)写出月利润f(x)(万元)关于月产量x(万件)的函数解析式
(Ⅱ)当月产量在[1,2e]万件时,求该公司在生产这种小型产品中所获得的月利润最大值(万元)及此时的月生成量值(万件).(注:月利润=月销售收入+月国家补助-月总成本)
考点:导数在最大值、最小值问题中的应用
专题:导数的综合应用
分析:(Ⅰ)由月利润=月销售收入+月国家补助-月总成本,即可列出函数关系式;
(2)利用导数判断函数的单调性,进而求出函数的最大值.
(2)利用导数判断函数的单调性,进而求出函数的最大值.
解答:
解:(Ⅰ)由于:月利润=月销售收入+月国家补助-月总成本,可得
(Ⅱ)f(x)=-x2+2(e+1)x-2elnx-2的定义域为[1,2e],
且f′(x)=-2x+2(e+1)-
=-
(x>0)
列表如下:
由上表得:f(x)=-x2+2(e+1)x-2elnx-2在定义域[1,2e]上的最大值为f(e).
且f(e)=e2-2.即:月生产量在[1,2e]万件时,该公司在生产这种小型产品中所获得的月利润最大值为f(e)=e2-2,此时的月生产量值为e(万件).
|
(Ⅱ)f(x)=-x2+2(e+1)x-2elnx-2的定义域为[1,2e],
且f′(x)=-2x+2(e+1)-
| 2e |
| x |
| 2(x-1)(x-e) |
| x |
列表如下:
| x | (1,e) | e | (e,2e] |
| f'(x) | + | 0 | - |
| f(x) | 增 | 极大值f(e) | 减 |
且f(e)=e2-2.即:月生产量在[1,2e]万件时,该公司在生产这种小型产品中所获得的月利润最大值为f(e)=e2-2,此时的月生产量值为e(万件).
点评:本题主要考查利用导数研究函数的单调性、求函数的最值等知识,考查学生利用导数解决实际问题的能力及运算求解能力,属于难题.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
已知全集U=R,集合A={y|y=lg(x2+10),x∈R),集合B={x||x-2|<1},则(∁UB)∩A=( )
| A、{x|0≤x<1或x>3} |
| B、{x|x=1或x≥3} |
| C、{x|x>3} |
| D、{x|1≤x≤3} |
已知函数f(x)=4x2-mx-8在[5,20]具有单调性,则实数的取值范围为( )
| A、(-∞,-160]∪[160,+∞) |
| B、(-∞,40]∪[160,+∞) |
| C、(-∞,-160]∪[40,+∞) |
| D、[40,160] |
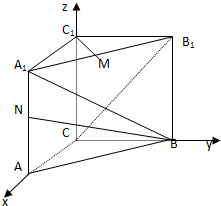 如图,直三棱柱ABC-A1B1C1的底面三角形ABC中,CA=CB=1,∠BCA=90°,棱AA1=2,M、N分别是A1B1、A1A的中点.
如图,直三棱柱ABC-A1B1C1的底面三角形ABC中,CA=CB=1,∠BCA=90°,棱AA1=2,M、N分别是A1B1、A1A的中点.