题目内容
在等差数列{an}中,Sn为其前n项和,且a5=9,S3=9.
(Ⅰ)求数列{an}的通项an;
(Ⅱ)设数列bn=
,求数列{bn}的前n项和Tn.
(Ⅰ)求数列{an}的通项an;
(Ⅱ)设数列bn=
| 1 |
| anan+1 |
考点:数列的求和,等差数列的通项公式
专题:等差数列与等比数列
分析:(Ⅰ)由题意列出方程组,解得首项及公差,即可求得通项公式;
(Ⅱ)bn=
=
=
(
-
),利用裂项法求和即可.
(Ⅱ)bn=
| 1 |
| anan+1 |
| 1 |
| (2n-1)(2n+1) |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
解答:
解:(Ⅰ)由已知得
,解得a1=1,d=2,∴an=2n-1
(Ⅱ)依题意有:bn=
=
=
(
-
),
于是:Tn=
×(1-
+
-
+
-
+…+
-
)=
×(1-
)=
.
|
(Ⅱ)依题意有:bn=
| 1 |
| anan+1 |
| 1 |
| (2n-1)(2n+1) |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
于是:Tn=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 5 |
| 1 |
| 7 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
| 1 |
| 2 |
| 1 |
| 2n+1 |
| n |
| 2n+1 |
点评:本题主要考查等差数列的通项公式及求和公式,考查学生利用裂项相消法求数列的和等知识,属于中档题,注意裂项的技巧.

练习册系列答案
相关题目
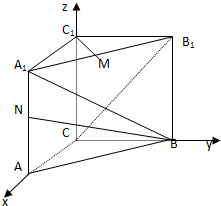 如图,直三棱柱ABC-A1B1C1的底面三角形ABC中,CA=CB=1,∠BCA=90°,棱AA1=2,M、N分别是A1B1、A1A的中点.
如图,直三棱柱ABC-A1B1C1的底面三角形ABC中,CA=CB=1,∠BCA=90°,棱AA1=2,M、N分别是A1B1、A1A的中点.