题目内容
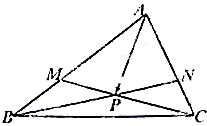在△ABC中，点M、N分别在边AB、AC上，且| AM |
| MB |
| AN |
| 3 |
| 5 |
| AC |
| AB |
| a |
| AC |
| b |
| AP |
| a |
| b |
A、
| ||||||||||
B、
| ||||||||||
C、
| ||||||||||
D、
|
考点：平面向量的基本定理及其意义
专题：平面向量及应用
分析：由B，P，N三点共线，得存在实数m，使
=m
+（1-m）
；M，P，C三点共线，得存在实数n，使
=n
+（1-n）
；再由向量相等，列方程组，求出m、n的值即可．
| AP |
| AB |
| AN |
| AP |
| AC |
| AM |
解答：
解：∵
=2
，
=
，∴
=
；
又∵B，P，N三点共线，∴存在实数m，使得
=m
+（1-m）
，即
=m
+
（1-m）
；
同理M，P，C三点共线，∴存在实数n，使得
=n
+（1-n）
，即
=n
+
（1-n）
；
由向量相等得，
，
解得m=
，n=
；
∴
=
+
×（1-
）
=
+
．
故选：A．
| AM |
| MB |
| AN |
| 3 |
| 5 |
| AC |
| AM |
| 2 |
| 3 |
| AB |
又∵B，P，N三点共线，∴存在实数m，使得
| AP |
| AB |
| AN |
| AP |
| AB |
| 3 |
| 5 |
| AC |
同理M，P，C三点共线，∴存在实数n，使得
| AP |
| AC |
| AM |
| AP |
| AC |
| 2 |
| 3 |
| AB |
由向量相等得，
|
解得m=
| 4 |
| 9 |
| 1 |
| 3 |
∴
| AP |
| 4 |
| 9 |
| AB |
| 3 |
| 5 |
| 4 |
| 9 |
| AC |
| 4 |
| 9 |
| a |
| 1 |
| 3 |
| b |
故选：A．
点评：本题考查了平面向量的基本定理的应用问题，解题的关键是根据三点共线，得出向量
的线性表示，列出方程组，是中档题．
| AP |
练习册系列答案
相关题目
已知函数f（x）=4x2-mx-8在[5，20]具有单调性，则实数的取值范围为（ ）
| A、（-∞，-160]∪[160，+∞） |
| B、（-∞，40]∪[160，+∞） |
| C、（-∞，-160]∪[40，+∞） |
| D、[40，160] |