题目内容
8.已知函数f(x)=|x-1|+|x-a|(1)若函数f(x)的值域为[2,+∞),求实数a的值
(2)若f(2-a)≥f(2),求实数a的取值范围.
分析 (1)利用函数的几何意义,求出函数的最小值,列出方程求解a即可.
(2)利用不等式,转化为代数不等式,求解即可.
解答 解:(1)∵函数f(x)=|x-1|+|x-a|≥|x-1-(x-a)|=|a-1|,
∴|a-1|=2,解得a=3或a=-1.
(2)由f(2-a)≥f(2),可得3|a-1|-|a-2|≥1,
则$\left\{\begin{array}{l}{a≤1}\\{3(1-a)-(2-a)≥1}\end{array}\right.$或$\left\{\begin{array}{l}{1≤a≤2}\\{3(a-1)-(2-a)≥1}\end{array}\right.$或$\left\{\begin{array}{l}{a≥2}\\{3(a-1)-(a-2)≥1}\end{array}\right.$,
解得:a≤0或$\frac{3}{2}≤a≤2$或a≥2.
综上a的范围是:$(-∞,0]∪[\frac{3}{2},+∞)$.
点评 本题考查函数的最值及函数恒成立,不等式的解法,考查分类讨论思想的应用.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
19.某四棱锥的三视图如图所示,则该四棱锥的侧面积为( )
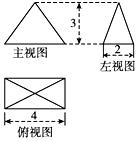

| A. | 8 | B. | 8+4$\sqrt{10}$ | C. | 4$\sqrt{10}$+2$\sqrt{13}$ | D. | 2$\sqrt{10}$+$\sqrt{13}$ |
3.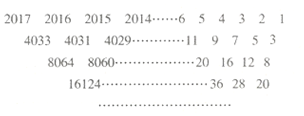 “杨辉三角”又称“贾宪三角”,是因为贾宪约在公元1050年首先使用“贾宪三角”进行高次开方运算,而杨辉在公元1261年所著的《详解九章算法》一书中,辑录了贾宪三角形数表,并称之为“开方作法本源”图.下列数表的构造思路就源于“杨辉三角”.该表由若干行数字组成,从第二行起,每一行中的数字均等于其“肩上”两数之和,表中最后一行仅有一个数,则这个数是( )
“杨辉三角”又称“贾宪三角”,是因为贾宪约在公元1050年首先使用“贾宪三角”进行高次开方运算,而杨辉在公元1261年所著的《详解九章算法》一书中,辑录了贾宪三角形数表,并称之为“开方作法本源”图.下列数表的构造思路就源于“杨辉三角”.该表由若干行数字组成,从第二行起,每一行中的数字均等于其“肩上”两数之和,表中最后一行仅有一个数,则这个数是( )
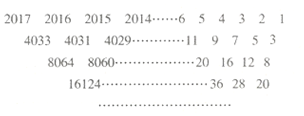 “杨辉三角”又称“贾宪三角”,是因为贾宪约在公元1050年首先使用“贾宪三角”进行高次开方运算,而杨辉在公元1261年所著的《详解九章算法》一书中,辑录了贾宪三角形数表,并称之为“开方作法本源”图.下列数表的构造思路就源于“杨辉三角”.该表由若干行数字组成,从第二行起,每一行中的数字均等于其“肩上”两数之和,表中最后一行仅有一个数,则这个数是( )
“杨辉三角”又称“贾宪三角”,是因为贾宪约在公元1050年首先使用“贾宪三角”进行高次开方运算,而杨辉在公元1261年所著的《详解九章算法》一书中,辑录了贾宪三角形数表,并称之为“开方作法本源”图.下列数表的构造思路就源于“杨辉三角”.该表由若干行数字组成,从第二行起,每一行中的数字均等于其“肩上”两数之和,表中最后一行仅有一个数,则这个数是( )| A. | 2017×22016 | B. | 2018×22015 | C. | 2017×22015 | D. | 2018×22016 |
20.已知a、b∈{2,3,4,5,6,7,8,9},则logab的不同取值个数为( )
| A. | 53 | B. | 56 | C. | 55 | D. | 57 |
17.在方程|x|+|y|=1表示的曲线所围成的区域内(包含边界)任取一点P(x,y),则z=xy的最大值为( )
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{8}$ |
18.已知函数f(x)=$\left\{\begin{array}{l}{lg(x+m),0<x<1}\\{\sqrt{x},x≥1}\end{array}\right.$在(0,+∞)上是增函数,则实数m的取值范围是( )
| A. | (-∞,9] | B. | (0,9] | C. | [0,9] | D. | [0,9) |