题目内容
15.已知命题$p:?x>e,{({\frac{1}{2}})^x}$>lnx;命题q:?a>1,b>1,logab+2logba≥2$\sqrt{2}$,则下列命题中为真命题的是( )| A. | (?p)∧q | B. | p∧q | C. | p∧(?q) | D. | p∨(?q) |
分析 命题$p:?x>e,{({\frac{1}{2}})^x}$<1<lnx,可得p是假命题;命题q:?a>1,b>1,logab,logba>0,转化为logab+2logba=logab+$\frac{2}{lo{g}_{a}b}$,利用基本不等式的性质即可判断出真假,再利用简易逻辑的判定方法即可得出.
解答 解:命题$p:?x>e,{({\frac{1}{2}})^x}$<1<lnx,因此是假命题;
命题q:?a>1,b>1,logab,logba>0,
∴logab+2logba=logab+$\frac{2}{lo{g}_{a}b}$≥2$\sqrt{lo{g}_{a}b•\frac{2}{lo{g}_{a}b}}$=2$\sqrt{2}$,当且仅当logab=$\sqrt{2}$时取等号.因此q是真命题.
则下列命题中为真命题的是(¬p)∧q.
故选:A.
点评 本题考查了简易逻辑的应用、函数的单调性、基本不等式的性质、转化方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
3.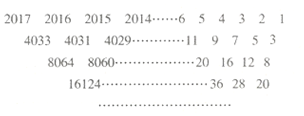 “杨辉三角”又称“贾宪三角”,是因为贾宪约在公元1050年首先使用“贾宪三角”进行高次开方运算,而杨辉在公元1261年所著的《详解九章算法》一书中,辑录了贾宪三角形数表,并称之为“开方作法本源”图.下列数表的构造思路就源于“杨辉三角”.该表由若干行数字组成,从第二行起,每一行中的数字均等于其“肩上”两数之和,表中最后一行仅有一个数,则这个数是( )
“杨辉三角”又称“贾宪三角”,是因为贾宪约在公元1050年首先使用“贾宪三角”进行高次开方运算,而杨辉在公元1261年所著的《详解九章算法》一书中,辑录了贾宪三角形数表,并称之为“开方作法本源”图.下列数表的构造思路就源于“杨辉三角”.该表由若干行数字组成,从第二行起,每一行中的数字均等于其“肩上”两数之和,表中最后一行仅有一个数,则这个数是( )
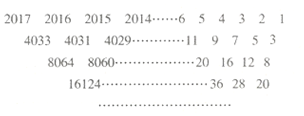 “杨辉三角”又称“贾宪三角”,是因为贾宪约在公元1050年首先使用“贾宪三角”进行高次开方运算,而杨辉在公元1261年所著的《详解九章算法》一书中,辑录了贾宪三角形数表,并称之为“开方作法本源”图.下列数表的构造思路就源于“杨辉三角”.该表由若干行数字组成,从第二行起,每一行中的数字均等于其“肩上”两数之和,表中最后一行仅有一个数,则这个数是( )
“杨辉三角”又称“贾宪三角”,是因为贾宪约在公元1050年首先使用“贾宪三角”进行高次开方运算,而杨辉在公元1261年所著的《详解九章算法》一书中,辑录了贾宪三角形数表,并称之为“开方作法本源”图.下列数表的构造思路就源于“杨辉三角”.该表由若干行数字组成,从第二行起,每一行中的数字均等于其“肩上”两数之和,表中最后一行仅有一个数,则这个数是( )| A. | 2017×22016 | B. | 2018×22015 | C. | 2017×22015 | D. | 2018×22016 |
10.下列命题中,正确的是( )
①?x∈R,2x>3x;②“x≠3”是“|x|≠3”成立的充分条件;③空间中若直线l若平行于平面α,则α内所有直线均与l是异面直线;④空间中有三个角是直角的四边形不一定是平面图形.
①?x∈R,2x>3x;②“x≠3”是“|x|≠3”成立的充分条件;③空间中若直线l若平行于平面α,则α内所有直线均与l是异面直线;④空间中有三个角是直角的四边形不一定是平面图形.
| A. | ①③ | B. | ①④ | C. | ②④ | D. | ②③ |
20.已知a、b∈{2,3,4,5,6,7,8,9},则logab的不同取值个数为( )
| A. | 53 | B. | 56 | C. | 55 | D. | 57 |
7.若f(x)是定义在R上的函数,且满足:①f(x)是偶函数;②f(x+2)是偶函数;③当0<x≤2时,f(x)=log2017x,当x=0时,f(0)=0,则方程f(x)=-2017在区间(1,10)内的多有实数根之和为( )
| A. | 0 | B. | 10 | C. | 12 | D. | 24 |
4.集合A={x∈N|x2-4x-5<0},B={x|log2(x-2)≤1},则A∩B=( )
| A. | (-1,4] | B. | (2,4] | C. | (3,4) | D. | {3,4} |