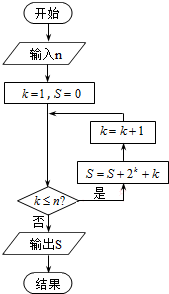
题目内容
 设a≠0,n是大于1的自然数,(1+
设a≠0,n是大于1的自然数,(1+| x |
| a |
考点:二项式定理的应用,二项式系数的性质
专题:二项式定理
分析:求出(1+
)n的展开式的通项为Tk+1=
(
)k=
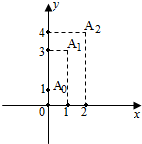
xk,由图知,a0=1,a1=3,a2=4,列出方程组,求出a的值.
| x |
| a |
| C | k n |
| x |
| a |
| 1 |
| ak |
| C | k n |
解答:
解:(1+
)n的展开式的通项为Tk+1=
(
)k=
xk,
由图知,a0=1,a1=3,a2=4,
∴
=3,
=4,
=3,
=4,
a2-3a=0,
解得a=3,
故答案为:3.
| x |
| a |
| C | k n |
| x |
| a |
| 1 |
| ak |
| C | k n |
由图知,a0=1,a1=3,a2=4,
∴
| 1 |
| a |
| C | 1 n |
| 1 |
| a2 |
| C | 2 n |
| n |
| a |
| n(n-1) |
| 2a2 |
a2-3a=0,
解得a=3,
故答案为:3.
点评:本题考查解决二项式的特定项问题,关键是求出展开式的通项,属于一道中档题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
若实数k满足0<k<5,则曲线
-
=1与
-
=1的( )
| x2 |
| 16 |
| y2 |
| 5-k |
| x2 |
| 16-k |
| y2 |
| 5 |
| A、实半轴长相等 |
| B、虚半轴长相等 |
| C、离心率相等 |
| D、焦距相等 |