题目内容
已知曲线C1的参数方程是
(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程是ρ=2,则C1与C2交点的直角坐标为 .
|
考点:点的极坐标和直角坐标的互化,参数方程化成普通方程
专题:直线与圆
分析:把参数方程、极坐标方程化为直角坐标方程,再把两曲线的方程联立方程组求得 C1与C2交点的直角坐标.
解答:
解:把曲线C1的参数方程是
(t为参数),消去参数化为直角坐标方程为x2=3y2 (x≥0,y≥0).
曲线C2的极坐标方程是ρ=2,化为直角坐标方程为x2+y2=4.
解方程组
,求得
,∴C1与C2交点的直角坐标为(
,1),
故答案为:(
,1).
|
曲线C2的极坐标方程是ρ=2,化为直角坐标方程为x2+y2=4.
解方程组
|
|
| 3 |
故答案为:(
| 3 |
点评:本题主要考查把参数方程、极坐标方程化为直角坐标方程的方法,求两条曲线的交点,属于基础题.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
 设a≠0,n是大于1的自然数,(1+
设a≠0,n是大于1的自然数,(1+ 设a是一个各位数字都不是0且没有重复数字三位数,将组成a的3个数字按从小到大排成的三位数记为I(a),按从大到小排成的三位数记为D(a)(例如a=815,则I(a)=158,D(a)=851),阅读如图所示的程序框图,运行相应的程序,任意输入一个a,输出的结果b=
设a是一个各位数字都不是0且没有重复数字三位数,将组成a的3个数字按从小到大排成的三位数记为I(a),按从大到小排成的三位数记为D(a)(例如a=815,则I(a)=158,D(a)=851),阅读如图所示的程序框图,运行相应的程序,任意输入一个a,输出的结果b=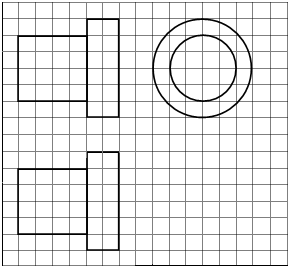 如图,网格纸上正方形小格的边长为1(表示1cm),图中粗线画出的是某零件的三视图,该零件由一个底面半径为3cm,高为6cm的圆柱体毛坯切削得到,则切削掉部分的体积与原来毛坯体积的比值为( )
如图,网格纸上正方形小格的边长为1(表示1cm),图中粗线画出的是某零件的三视图,该零件由一个底面半径为3cm,高为6cm的圆柱体毛坯切削得到,则切削掉部分的体积与原来毛坯体积的比值为( )