题目内容
若实数k满足0＜k＜5，则曲线
-
=1与
-
=1的（ ）
| x2 |
| 16 |
| y2 |
| 5-k |
| x2 |
| 16-k |
| y2 |
| 5 |
| A、实半轴长相等 |
| B、虚半轴长相等 |
| C、离心率相等 |
| D、焦距相等 |
考点：双曲线的简单性质
专题：圆锥曲线的定义、性质与方程
分析：根据k的取值范围，判断曲线为对应的双曲线，以及a，b，c的大小关系即可得到结论．
解答：
解：当0＜k＜5，则0＜5-k＜5，11＜16-k＜16，
即曲线
-
=1表示焦点在x轴上的双曲线，其中a2=16，b2=5-k，c2=21-k，
曲线
-
=1表示焦点在x轴上的双曲线，其中a2=16-k，b2=5，c2=21-k，
即两个双曲线的焦距相等，
故选：D．
即曲线
| x2 |
| 16 |
| y2 |
| 5-k |
曲线
| x2 |
| 16-k |
| y2 |
| 5 |
即两个双曲线的焦距相等，
故选：D．
点评：本题主要考查双曲线的方程和性质，根据不等式的范围判断a，b，c是解决本题的关键．
练习册系列答案
相关题目
设a≠0，n是大于1的自然数，（1+在△ABC中，角A、B、C所对应的边分别为a，b，c，则“a≤b”是“sinA≤sinB”的（ ）
| A、充分必要条件 |
| B、充分非必要条件 |
| C、必要非充分条件 |
| D、非充分非必要条件 |
设a，b是关于t的方程t2cosθ+tsinθ=0的两个不等实根，则过A（a，a2），B（b，b2）两点的直线与双曲线
-
=1的公共点的个数为（ ）
| x2 |
| cos2θ |
| y2 |
| sin2θ |
| A、0 | B、1 | C、2 | D、3 |
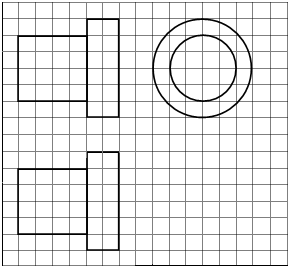如图，网格纸上正方形小格的边长为1（表示1cm），图中粗线画出的是某零件的三视图，该零件由一个底面半径为3cm，高为6cm的圆柱体毛坯切削得到，则切削掉部分的体积与原来毛坯体积的比值为（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
设U为全集，A，B是集合，则“存在集合C使得A⊆C，B⊆∁UC”是“A∩B=∅”的（ ）
| A、充分而不必要的条件 |
| B、必要而不充分的条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知向量
=（1，2），
=（3，1），则
-
=（ ）
| a |
| b |
| b |
| a |
| A、（-2，1） |
| B、（2，-1） |
| C、（2，0） |
| D、（4，3） |