题目内容
已知p:-1<2x-3<1,q:x(x-3)<0,则p是q的什么条件( )
| A、必要不充分 |
| B、充分不必要 |
| C、充要 |
| D、既不充分也不必要 |
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:先通过解一元一次不等式,一元二次不等式求出p,q下的x的范围,然后根据充分条件、必要条件的概念即可判断出p是q的什么条件.
解答:
解:p:1<x<2,q:0<x<3;
∴p能得到q,而q得不到p;
∴p是q的充分不必要条件.
故选B.
∴p能得到q,而q得不到p;
∴p是q的充分不必要条件.
故选B.
点评:考查解一元一次不等式,一元二次不等式,以及充分条件、必要条件、充分不必要条件的概念.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
直线y=kx-2与椭圆x2+4y2=80相交于不同的两点P、Q,若PQ的中点横坐标为2,则直线的斜率等于( )
A、
| ||
B、
| ||
| C、2 | ||
| D、4 |
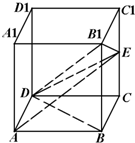 在棱长为2的正方体ABCD-A1B1C1D1中,设E是棱CC1的中点.
在棱长为2的正方体ABCD-A1B1C1D1中,设E是棱CC1的中点.